중력 방향 바꾸기
Change of Gravity Direction
김명호(MyungHo Kim, mkim1795 - gmail.com)
* 아인슈타인이 수정한 뉴튼 제2법칙, Lorentz 전환 불변
\begin{equation}
\begin{aligned}
즉\, 입자가\, x\, 축\, 상에서만\, 움직이는\, 경우,
\,F=\frac{dm{\frac{dx}{dt}}}{dt} =\frac{dm{\frac{dx'}{dt'}}}{dt'}=F' 입증
(여기서\, m=\frac{m_0}{\sqrt{A}},
\,A=1-\frac{(\frac{dx}{dt})^2}{c^2})
\\
\frac{dx'}{dt'}=\frac{\frac{dx'}{dt}}{\frac{dt'}{dt}}
=\frac{\frac{\partial x'}{\partial t}\frac{dt}{dt}+\frac{\partial x'}{\partial x}\frac{dx}{dt}}
{\frac{\partial t'}{\partial t}\frac{dt}{dt}+\frac{\partial t'}{\partial x}\frac{dx}{dt}}
=\frac{\frac{-u}{\sqrt \alpha}+\frac{1}{\sqrt \alpha}\frac{dx}{dt}}
{\frac{1}{\sqrt \alpha}-\frac{u}{c^2\sqrt \alpha}\frac{dx}{dt}}
=\frac{-u+\frac{dx}{dt}}{1-\frac{u}{c^2}\frac{dx}{dt}}
=\frac{-u+\frac{dx}{dt}}{\beta} \,\,\,\,\, (1)
\\여기서\, x'=\frac{x-ut}{\sqrt\alpha},\, t'=\frac{t-\frac{ux}{c^2}}{\sqrt{\alpha}},\, \alpha=1-\frac{u^2}{c^2},\, \beta=1-\frac{u}{c^2}\frac{dx}{dt}
\\ \frac{d^2x'}{dt'^2}=\frac{d\frac{dx'}{dt'}}{dt'}
=\frac{\frac{d(\frac{-u+\frac{dx}{dt}}{\beta})}{dt}}
{\frac{dt'}{dt}}
=\frac{\frac{\frac{dx^2}{dt^2}\beta+\frac{u}{c^2}\frac{dx^2}{dt^2}(-u+\frac{dx}{dt})}{\beta^2}}
{\frac{1}{\sqrt{\alpha}}-\frac{u}{c^2\sqrt{\alpha}}\frac{dx}{dt}}
=\frac{\frac{d^2x}{dt^2}-\frac{u^2}{c^2}\frac{d^2x}{dt^2}}{\beta^2(\frac{1}{\sqrt{\alpha}}-\frac{u}{c^2\sqrt{\alpha}}\frac{dx}{dt})}
=\alpha^{\frac{3}{2}}\frac{\frac{d^2x}{dt^2}}{\beta^3}\,\,\,(2)
\\(1)과\, (2)를\, 대입하면,
\\ \frac{dA^{-\frac{1}{2}}}{dt}=-\frac{A^{-\frac{3}{2}}}{2}\frac{dA}{dt} =-\frac{A^{-\frac{3}{2}}}{2}(-\frac{2}{c^2}\frac{dx}{dt}\frac{d^2x}{dt^2})
=\frac{1}{c^2A^{\frac32}}\frac{dx}{dt}\frac{d^2x}{dt^2}
\\=> F=\frac{dm\frac{dx}{dt}}{dt}=m_0\frac{d}{dt}(A^{-\frac{1}{2}}\frac{dx}{dt})
=m_0\frac{dA^{-\frac{1}{2}}}{dt}\frac{dx}{dt}+m_0A^{-\frac{1}{2}}\frac{d^2x}{dt^2}
\\=m_0\frac{1}{c^2A^{\frac32}}(\frac{dx}{dt})^2\frac{d^2x}{dt^2}+m_0A^{-\frac{1}{2}}\frac{d^2x}{dt^2}
=m_0\frac{1}{c^2A^{\frac32}}\frac{d^2x}{dt^2}((\frac{dx}{dt})^2+c^2A)=\frac{m_0}{A^{\frac32}}\frac{d^2x}{dt^2}\,\,\,(3)
\end{aligned}
\end{equation}
그리고
\begin{equation}
\begin{aligned}
A'=1-\frac{(\frac{dx'}{dt'})}{c^2}
=1-\frac{(-u+\frac{dx}{dt})^2}{\beta^2c^2{}}
=\frac{c^2 (1-\frac{u}{c^2}\frac{dx}{dt})^2 - (-u+\frac{dx}{dt})^2}
{\beta^2c^2}
=\frac{\alpha(c^2-(\frac{dx}{dt})^2)}{\beta^2c^2}
=\frac{\alpha A} {\beta^2}
\\=> {A'}^\frac{3}{2}= \frac{\alpha^\frac32 A^\frac32}{\beta^3}\,\,\,(4)
\end{aligned}
\end{equation}
(2), (3) (4)를 대입하여
\begin{equation}
F'=\frac{dm\frac{dx'}{dt'}}{dt'}=\frac{m_0}{A'^{\frac32}} \frac{d^2x'}{d{t'}^2}
= \frac{m_0}{A'^{\frac32}} \alpha^{\frac{3}{2}}\frac{\frac{d^2x}{dt^2}}{\beta^3}
=\frac{m_0}{A^{\frac32}}\frac{d^2x}{dt^2}=F\,\, 증명\, 끝.
\end{equation}
=> 일반적인 경우의 증명
\begin{equation}
\begin{aligned}
\frac{1}{4\pi\epsilon_0} \,당분간\,생략,\, S(a+)=infinitesimally\, 얇은\, 구
\\\int_{S(a+)} \frac{(c-z)\sigma_0\cos\phi}{({x^{2}+y^{2}+(c-z)^2})^{\frac32}} dV
=\sigma_0\int_{S(a+)} \frac{(c-z)\cos\phi}{({a^2+c^2-2cz})^{\frac32}} dV
=\sigma_0\int_{S(a+)} \frac{(c-r\cos\phi)\cos\phi}{({a^2+c^2-2cr\cos\phi})^{\frac32}}r^2 \sin\phi d\theta d\phi dr \\
=\sigma_0\int_a^{a+\Delta{r}}\int_0^\pi\int_0^{2\pi} r^2\frac{(c-r\cos\phi)\cos\phi}{({a^2+c^2-2cr\cos\phi})^{\frac32}} \sin\phi d\theta d\phi dr
={2\pi}\sigma_0\int_a^{a+\Delta{r}}\int_0^\pi r^2\frac{(c-r\cos\phi)\cos\phi}{({a^2+c^2-2cr\cos\phi})^{\frac32}} \sin\phi d\phi dr=
\\let\,u=\cos\phi, \frac{du}{dt}= -\sin\phi\, => {2\pi}\sigma_0\int_a^{a+\Delta{r}}r^2\int_1^{-1} \frac{(c-ru)u}{({a^2+c^2-2cru})^{\frac32}} (-du) dr\\= {2\pi}\sigma_0\int_{-1}^1\int_a^{a+\Delta{r}}r^2 \frac{(c-ru)u}{({a^2+c^2-2cru})^{\frac32}} dr du=
{2\pi}\sigma_0\int_{-1}^1 a^2 \frac{(c-au)u}{({a^2+c^2-2cau})^{\frac32}}\Delta{r} du,
\\let\, t=({a^2+c^2-2acu})^{\frac12}\, => t^2={a^2+c^2-2acu},\, => u=\frac{a^2+c^2-t^2}{2ac},\,c>a라\, 가정, c-a\leq t \leq c+a, \,
\\tdt=-acdu\, => du=\frac{-tdt}{ac}\, 그래서
\\=>\, {2\pi}\sigma_0\int_{-1}^1 a^2 \frac{(c-au)u}{({a^2+c^2-2cau})^{\frac32}}\Delta{r} du=
{2\pi}\sigma_0 a^2\Delta{r}\int_{c+a}^{c-a} \frac{(c-a\frac{a^2+c^2-t^2}{2ac})\frac{a^2+c^2-t^2}{2ac}}{t^3} \frac{-tdt}{ac}
\\={2\pi}\sigma_0 a^2\Delta{r}\int_{c+a}^{c-a} \frac{(\frac{c^2-a^2+t^2}{2c})\frac{a^2+c^2-t^2}{2ac}}{t^2} \frac{-dt}{ac}
={2\pi}\sigma_0 a^2\Delta{r}\int_{c+a}^{c-a} \frac{(\frac{c^4-(a^2-t^2)^2}{4ac^2})}{t^2} \frac{-dt}{ac}
\\={2\pi}\sigma_0 a^2\Delta{r}\int_{c-a}^{c+a} \frac{c^4-(a^2-t^2)^2}{4a^2c^3t^2} dt....(*)
\\=\frac{{\pi}\sigma_0}{2c^3} \Delta{r}\int_{c-a}^{c+a} \frac{c^4-(a^2-t^2)^2}{t^2} dt
=\frac{{\pi}\sigma_0}{2c^3} \Delta{r}\int_{c-a}^{c+a} \frac{c^4-(a^2-t^2)^2}{t^2} dt
=\frac{{\pi}\sigma_0}{2c^3} \Delta{r}\int_{c-a}^{c+a} \frac{c^4-a^4}{t^2} +2a^2-t^2 dt
\\=\frac{{\pi}\sigma_0}{2c^3} \Delta{r}( - \frac{c^4-a^4}{t}\Biggr|_{c-a}^{c+a} +4a^3-\frac{t^3}3\Biggr|_{c-a}^{c+a})
=\frac{{\pi}\sigma_0}{2c^3} \Delta{r}( - \frac{c^4-a^4}{c+a}+\frac{c^4-a^4}{c-a} +4a^3-\frac{(c+a)^3}3+\frac{(c-a)^3}3)
\\=\frac{{\pi}\sigma_0}{2c^3} \Delta{r}[2a(c^2+a^2)+4a^3-\frac{2a^3+6c^2a}3]=\frac{{\pi}\sigma_0}{2c^3} \Delta{r}\frac{16}3a^3
=\frac{8{\pi}\sigma_0 a^3}{3c^3} \Delta{r}
\\생략한\, \frac{1}{4\pi\epsilon_0}를\, 곱하면,\, \frac{1}{4\pi\epsilon_0}\frac{8{\pi}\sigma_0 a^3}{3c^3} \Delta{r}=\frac{2\sigma_0 a^3}{3\epsilon_0c^3} \Delta{r}...
\\E_z=\frac{p}{4\pi\epsilon_0}\,\frac{3\cos^2\theta-1}{r^3}에\, \theta=0, \,r=c와\, p=\frac{4\pi\sigma_0 a^3}{3}를\, 대입하면\, 나오는\, 값,\, 차이는\, \Delta{r}
\end{aligned}
\end{equation}
Δ r =d, 즉 'infinitesimal unit'.
c가 a 보다 작은 경우 즉,
\begin{equation}
\begin{aligned}
위 (*) => {2\pi}\sigma_0 a^2\Delta{r}\int_{a-c}^{a+c} \frac{c^4-(a^2-t^2)^2}{4a^2c^3t^2} dt=\frac{{\pi}\sigma_0}{2c^3} \Delta{r}( - \frac{c^4-a^4}{t}\Biggr|_{a-c}^{a+c} +2a^2\Biggr|_{a-c}^{a+c}-\frac{t^3}3\Biggr|_{a-c}^{a+c})
\\=\frac{{\pi}\sigma_0}{2c^3} \Delta{r}(-2a^2c-2c^3+4a^2c-\frac{2c^3+6a^2c}3)=\frac{{\pi}\sigma_0}{2c^3} \Delta{r}(-\frac{8c^3}3)
=-\frac{4{\pi}\sigma_0\Delta{r}}3\,
생략한\, \frac{1}{4\pi\epsilon_0}를\, 곱하면\, -\frac{\sigma_0\Delta{r}}{3\epsilon_0},
\end{aligned}
\end{equation}
* 여기서 주목할 것은 전기장은 c=a에서 불연속이고 그 점을 지나며 부호가 달라지며 상수.
\begin{equation}
\begin{aligned}
b^2+c^2\leq{a^2}인\, 경우
\int_{S(a+)} \frac{(b-y)\sigma_0\cos\phi}{({x^{2}+y^{2}+(c-z)^2})^{\frac32}} dV=0\, 이라는\, 것.
\end{aligned}
\end{equation}
* 그린/스토크(Green/Stoke) 정리 증명(파인만 강의 II, 3-3)
 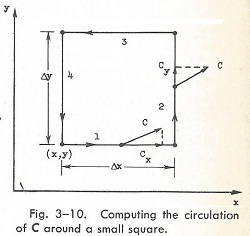
파인만은 뉴튼의 접근방법에 따라 미세하게 잘게 쪼개고 그들 합의 극한을 취하는 적분의 기본 정의, 즉 Riemann sum을 활용했다(위 그림, 참조: 파인만은 path integral 연구에도 Riemann sum을 기막히게 적용)
그림 3-10의 사각형 선을 따라 line integral을 하면
\begin{equation}
\simeq c_x(x, y)\Delta x+c_y(x+\Delta x,y)\Delta y-c_x(x+\Delta x, y+\Delta y)\Delta x-c_y(x, y+\Delta y)\Delta y
\\=-[c_x(x+\Delta x, y+\Delta y)-c_x(x,y)]\Delta x
+[c_y(x+\Delta x, y)-c_y(x, y+\Delta y)]\Delta y
\\=-[c_x(x+\Delta x, y+\Delta y)-c_x(x+\Delta x, y)+ c_x(x+\Delta x, y)- c_x(x,y)]\Delta x
\\+[c_y(x+\Delta x, y)-c_y(x, y)+c_y(x, y)- c_y(x, y+\Delta y)]\Delta y
\\= -[\frac{\partial C_x}{\partial y}(x+\Delta x, y)\Delta y+O(\Delta y) +\frac{\partial C_x}{\partial x}(x, y)\Delta x+ O(\Delta x)]\Delta x
\\+[\frac{\partial C_y}{\partial x}(x,y)\Delta x+O(\Delta x) -\frac{\partial C_y}{\partial y}(x,y)\Delta y+O(\Delta y) ]\Delta y
\\=-[\frac{\partial C_x}{\partial y}(x, y)\Delta y+O(\Delta x)\Delta y+ O(\Delta y)+\frac{\partial C_x}{\partial x}(x, y)\Delta x+ O(\Delta x)]\Delta x
\\+[\frac{\partial C_y}{\partial x}(x,y)\Delta x+O(\Delta x) -\frac{\partial C_y}{\partial y}(x,y)\Delta y+O(\Delta y) ]\Delta y
\\=> \lim_{M, N->\infty} \sum_{m, n=0}^{M,N}-\frac{\partial C_x}{\partial y}(x_m, y_n)+\frac{\partial C_y}{\partial x}(x_m, y_n){\Delta x}{\Delta y}
= \int\int-\frac{\partial C_x}{\partial y}+\frac{\partial C_y}{\partial x}dxdy,
\\ O(\Delta x),\, O(\Delta y)들\, 포함\, 항들 \to 0이니.
\\헌데, \, -\frac{\partial C_x}{\partial y}+\frac{\partial C_y}{\partial x}는\, \nabla \times C의\, z축\, 방향,\, 즉 \,(\nabla \times C)\cdot n,\,\, 따라서
\oint_{\Gamma}C\cdot ds=\int_S (\nabla \times C)\cdot n da
\end{equation}
* 리만 논문
요즘도 그런지 모르겠지만, 80년대 미국 대부분 대학에서처럼 오하이오(Ohio State University) 수학과는 박사과정에서 2개의 외국어 독해능력을 요구했다. 불어, 독어를 택했는데, 독해 능력 평가방법은 2가지, 해당 언어학과의 기초과정 과목을 3쿼터 수강하여 평점 B이상 받거나 언어담당 수학과 교수가 인정하는 교재 100페이지에서 출제하는 지문 번역 시험에 통과하는 것(* 교재는 학생이 선택할 수 있지만, 수학과 교수의 허가가 필요하다. 허가하면 교수와 상의하여 100 페이지를 정하고 교수는 그 100 페이지내에서 임의의 지문을 선택하여 언어학과로 보낸다. 그러면 시험 감독 및 채점한 언어학과에서 통과여부를 수학과에 통보).
불어는 어찌어찌 시험통과하고... 아~ 공포의 독일어! 75년도 서울대 본고사 제2외국어 독어 시험(50점 만점)에서 객관식은 문제 읽어보지도 않고 찍었다. 아마도 10점은 넘었으리라, 고3 독어 시험때 마다 그래왔는데 항상 10점 넘었으니 말이다.
그런 공포의 독일어를 다시 한번 해보자고 기초과목 신청하고 첫수업에 갔더니... 이상한 자부심 갖는 인간들이 그렇듯이*,
이 강사라는 놈이 여간 갈구는 게 아니다. 학점에 대한 출석, 숙제, 중간/학기말 시험들의 비율을 빡빡하게 정하고 이 과목은 'tough, tough...'*하다며 공포심 조장하며 수업 중 질문까지 해대지 않는가? 얼굴 마주칠까 고개 처박고 있는데도 옆에 와서 손으로 치면서... 못 살겠다....첫수업 끝나자 마자 '이 놈 밑에서 B 받으려다 그 과정 중의 스트레스로 죽을 것 같다' 판단하고 시험으로 전략 수정.
택한 교재*가 리만 논문집(Gesammelte Mathematische Werke, Wissenschaftlicher Nachlass und Nachträge - Collected Papers)이었고 열심 열심. 헌데, 하다보니 리만의 수학 접근 방법이 그동안 배워왔던 것과 아주 많이 다른 경험직관적... 은근 재미. 하여 시간 남을 때 끄적거린 거임.
'그렇듯이'에 대하여
외국인 조교(teaching assistant) 대부분이 들어야 하는 기초 영어과목의 강사 중에 한 놈이 꼭 그랬다. 미국은 물론 영어에 대한 자부심이 아주 대단. 학생이 영어에 대하여 조금이라도 흠을 얘기하면 흥분하는 인간이었다. 한번은 강의 중에 '미국이 스페인에게 쌀을 원조했다'라는 식의 예문을 썼단다. '그게 사실이냐?' 물었더니 모른댄다. '그럼 학생들이 오해하게 왜 그런 예문을 드느냐'고 따진 재밌는 선배가 있었다... 보아하니 강사가 one-eyed Jack처럼 검은 안대를 하고 다니는데, 눈은 멀쩡한 거라.. 하여 궁금함을 못 참는 선배가 '안대 왜 하고 다니냐?'고 했더니 '한눈으로 보면 일목 요연하다'라던 그런 인간.
'tough'에 대하여
한국 유학생들 중 이 단어를 입에 달고 사는 인간들이 꽤 많았다, '너희과는... 우리과는 터프해'.
과외 학생 부모가 '아~ 우리애가 머리는 좋은데 공부를 안 해요. 우리애가 창의력은 있는데 외우는 걸 잘 못해요.'를 듣는 기분. 하긴 좋아서 하는 게 아니라, 재미없는 공부를 '학위 증' 받으려고 좋지도 않은 머리 굴리려고 안간힘 쓰니 그럴 수 밖에.
'택하게 된 동기'
아인슈타인이 1905년 특수상대성 이론 발표하고 리만의 생각만이 옳았다고 했다. 그 관련 (Gauss를 흥분시킨) 리만의 기하 논문, 'Ueber die Hypothesen, welche der Geometrie zu Grunde liegen'이 많은 기하 논문/책에 줄기차게 인용되기에 '도대체 뭐냐?'며 궁금(* 내가 아는 한, 실제로 읽어본 인간들은 거의 없었다.) 적극적인 유태인들 후원으로 대중 스타까지 된 아인슈타인에 의해 세계적인 주목 받기 전엔 주로 이태리 수학자들만이 리만의 기하학 아이디어를 파고 들었었다.
|