39 The Kinetic Theory of Gases
The Kinetic Theory of Gases
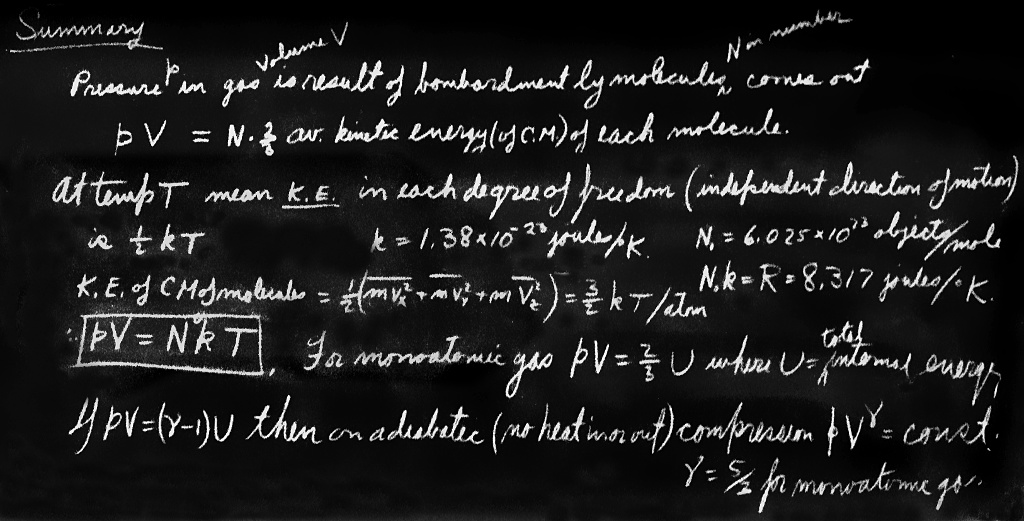
39–1Properties of matter
With this chapter we begin a new subject which will occupy us for some time. It is the first part of the analysis of the properties of matter from the physical point of view, in which, recognizing that matter is made out of a great many atoms, or elementary parts, which interact electrically and obey the laws of mechanics, we try to understand why various aggregates of atoms behave the way they do.
It is obvious that this is a difficult subject, and we emphasize at the beginning that it is in fact an extremely difficult subject, and that we have to deal with it differently than we have dealt with the other subjects so far. In the case of mechanics and in the case of light, we were able to begin with a precise statement of some laws, like Newton’s laws, or the formula for the field produced by an accelerating charge, from which a whole host of phenomena could be essentially understood, and which would produce a basis for our understanding of mechanics and of light from that time on. That is, we may learn more later, but we do not learn different physics, we only learn better methods of mathematical analysis to deal with the situation.
We cannot use this approach effectively in studying the properties of matter. We can discuss matter only in a most elementary way; it is much too complicated a subject to analyze directly from its specific basic laws, which are none other than the laws of mechanics and electricity. But these are a bit too far away from the properties we wish to study; it takes too many steps to get from Newton’s laws to the properties of matter, and these steps are, in themselves, fairly complicated. We will now start to take some of these steps, but while many of our analyses will be quite accurate, they will eventually get less and less accurate. We will have only a rough understanding of the properties of matter.
One of the reasons that we have to perform the analysis so imperfectly is that the mathematics of it requires a deep understanding of the theory of probability; we are not going to want to know where every atom is actually moving, but rather, how many move here and there on the average, and what the odds are for different effects. So this subject involves a knowledge of the theory of probability, and our mathematics is not yet quite ready and we do not want to strain it too hard.
Secondly, and more important from a physical standpoint, the actual behavior of the atoms is not according to classical mechanics, but according to quantum mechanics, and a correct understanding of the subject cannot be attained until we understand quantum mechanics. Here, unlike the case of billiard balls and automobiles, the difference between the classical mechanical laws and the quantum-mechanical laws is very important and very significant, so that many things that we will deduce by classical physics will be fundamentally incorrect. Therefore there will be certain things to be partially unlearned; however, we shall indicate in every case when a result is incorrect, so that we will know just where the “edges” are. One of the reasons for discussing quantum mechanics in the preceding chapters was to give an idea as to why, more or less, classical mechanics is incorrect in the various directions.
Why do we deal with the subject now at all? Why not wait half a year, or a year, until we know the mathematics of probability better, and we learn a little quantum mechanics, and then we can do it in a more fundamental way? The answer is that it is a difficult subject, and the best way to learn is to do it slowly! The first thing to do is to get some idea, more or less, of what ought to happen in different circumstances, and then, later, when we know the laws better, we will formulate them better.
Anyone who wants to analyze the properties of matter in a real problem might want to start by writing down the fundamental equations and then try to solve them mathematically. Although there are people who try to use such an approach, these people are the failures in this field; the real successes come to those who start from a physical point of view, people who have a rough idea where they are going and then begin by making the right kind of approximations, knowing what is big and what is small in a given complicated situation. These problems are so complicated that even an elementary understanding, although inaccurate and incomplete, is worthwhile having, and so the subject will be one that we shall go over again and again, each time with more and more accuracy, as we go through our course in physics.
Another reason for beginning the subject right now is that we have already used many of these ideas in, for example, chemistry, and we have even heard of some of them in high school. It is interesting to know the physical basis for these things.
As an interesting example, we all know that equal volumes of gases, at the same pressure and temperature, contain the same number of molecules. The law of multiple proportions, that when two gases combine in a chemical reaction the volumes needed always stand in simple integral proportions, was understood ultimately by Avogadro to mean that equal volumes have equal numbers of atoms. Now why do they have equal numbers of atoms? Can we deduce from Newton’s laws that the number of atoms should be equal? We shall address ourselves to that specific matter in this chapter. In succeeding chapters, we shall discuss various other phenomena involving pressures, volumes, temperature, and heat.
We shall also find that the subject can be attacked from a nonatomic point of view, and that there are many interrelationships of the properties of substances. For instance, when we compress something, it heats; if we heat it, it expands. There is a relationship between these two facts which can be deduced independently of the machinery underneath. This subject is called thermodynamics. The deepest understanding of thermodynamics comes, of course, from understanding the actual machinery underneath, and that is what we shall do: we shall take the atomic viewpoint from the beginning and use it to understand the various properties of matter and the laws of thermodynamics.
Let us, then, discuss the properties of gases from the standpoint of Newton’s laws of mechanics.
39–2The pressure of a gas
First, we know that a gas exerts a pressure, and we must clearly understand what this is due to. If our ears were a few times more sensitive, we would hear a perpetual rushing noise. Evolution has not developed the ear to that point, because it would be useless if it were so much more sensitive—we would hear a perpetual racket. The reason is that the eardrum is in contact with the air, and air is a lot of molecules in perpetual motion and these bang against the eardrums. In banging against the eardrums they make an irregular tattoo—boom, boom, boom—which we do not hear because the atoms are so small, and the sensitivity of the ear is not quite enough to notice it. The result of this perpetual bombardment is to push the drum away, but of course there is an equal perpetual bombardment of atoms on the other side of the eardrum, so the net force on it is zero. If we were to take the air away from one side, or change the relative amounts of air on the two sides, the eardrum would then be pushed one way or the other, because the amount of bombardment on one side would be greater than on the other. We sometimes feel this uncomfortable effect when we go up too fast in an elevator or an airplane, especially if we also have a bad cold (when we have a cold, inflammation closes the tube which connects the air on the inside of the eardrum with the outside air through the throat, so that the two pressures cannot readily equalize).
In considering how to analyze the situation quantitatively, we imagine that we have a volume of gas in a box, at one end of which is a piston which can be moved (Fig. 39–1). We would like to find out what force on the piston results from the fact that there are atoms in this box. The volume of the box is $V$, and as the atoms move around inside the box with various velocities they bang against the piston. Suppose there is nothing, a vacuum, on the outside of the piston. What of it? If the piston were left alone, and nobody held onto it, each time it got banged it would pick up a little momentum and it would gradually get pushed out of the box. So in order to keep it from being pushed out of the box, we have to hold it with a force $F$. The problem is, how much force? One way of expressing the force is to talk about the force per unit area: if $A$ is the area of the piston, then the force on the piston will be written as a number times the area. We define the pressure, then, as equal to the force that we have to apply on a piston, divided by the area of the piston:\begin{equation} \label{Eq:I:39:1} P = F/A. \end{equation} To make sure we understand the idea (we have to derive it for another purpose anyway), the differential work $dW$ done on the gas in compressing it by moving the piston in a differential amount $-dx$ would be the force times the distance that we compress it, which, according to (39.1), would be the pressure times the area, times the distance, which is equal to minus the pressure times the change in the volume: \begin{equation} \label{Eq:I:39:2} dW = F(-dx) = -PA\,dx = -P\,dV. \end{equation} (The area $A$ times the distance $dx$ is the volume change.) The minus sign is there because, as we compress it, we decrease the volume; if we think about it we can see that if a gas is compressed, work is done on it.
How much force do we have to apply to balance the banging of the molecules? The piston receives from each collision a certain amount of momentum. A certain amount of momentum per second will pour into the piston, and it will start to move. To keep it from moving, we must pour back into it the same amount of momentum per second from our force. Of course, the force is the amount of momentum per second that we must pour in. There is another way to put it: if we let go of the piston it will pick up speed because of the bombardments; with each collision we get a little more speed, and the speed thus accelerates. The rate at which the piston picks up speed, or accelerates, is proportional to the force on it. So we see that the force, which we already have said is the pressure times the area, is equal to the momentum per second delivered to the piston by the colliding molecules.
To calculate the momentum per second is easy—we can do it in two parts: first, we find the momentum delivered to the piston by one particular atom in a collision with the piston, then we have to multiply by the number of collisions per second that the atoms have with the wall. The force will be the product of these two factors. Now let us see what the two factors are: In the first place, we shall suppose that the piston is a perfect “reflector” for the atoms. If it is not, the whole theory is wrong, and the piston will start to heat up and things will change, but eventually, when equilibrium has set in, the net result is that the collisions are effectively perfectly elastic. On the average, every particle that comes in leaves with the same energy. So we shall imagine that the gas is in a steady condition, and we lose no energy to the piston because the piston is standing still. In those circumstances, if a particle comes in with a certain speed, it comes out with the same speed and, we will say, with the same mass.
If $\FLPv$ is the velocity of an atom, and $v_x$ is the $x$-component of $\FLPv$, then $mv_x$ is the $x$-component of momentum “in”; but we also have an equal component of momentum “out,” and so the total momentum delivered to the piston by the particle, in one collision, is $2mv_x$, because it is “reflected.”(다른 예: 힘과 모멘텀 관계)
Now, we need the number of collisions made by the atoms in a second, or in a certain amount of time $dt$; then we divide by $dt$. How many atoms are hitting? Let us suppose that there are $N$ atoms in the volume $V$, or $n = N/V$ in each unit volume(* 엄밀하게 따지자면, 각 입자마다 차지하는 부피에 해당하는 상수 곱하기가 빠져있는데, 별거 아닌 것처럼 보이는 이런 것들이 이론 전개를 밀어붙이는 힘이다). To find how many atoms hit the piston, we note that, given a certain amount of time $t$, if a particle has a certain velocity toward the piston it will hit during the time $t$, provided it is close enough. If it is too far away, it goes only part way toward the piston in the time $t$, but does not reach the piston. Therefore it is clear that only those molecules which are within a distance $v_xt$ from the piston are going to hit the piston in the time $t$. Thus the number of collisions in a time $t$ is equal to the number of atoms which are in the region within a distance $v_xt$, and since the area of the piston is $A$, the volume occupied by the atoms which are going to hit the piston is $v_xtA$.
21.10.18: analyze 접근 방법 => 증발과 액화, 접촉경계부분
2023.9.27: 단위 시간내에 도착한 입자들 갯수 센다는 건 아주 중요한 착안이라 자주 나온다
So we find that the force is \begin{equation} \label{Eq:I:39:3} F = nv_xA\cdot 2mv_x. \end{equation} See, the force is proportional to the area, if we keep the particle density fixed as we change the area! The pressure is then \begin{equation} \label{Eq:I:39:4} P = 2nmv_x^2. \end{equation}
Now we notice a little trouble with this analysis: First, all the molecules do not have the same velocity, and they do not move in the same direction. So, all the $v_x^2$’s are different! So what we must do, of course, is to take an average of the $v_x^2$’s, since each one makes its own contribution. What we want is the square of $v_x$, averaged over all the molecules: \begin{equation} \label{Eq:I:39:5} P = nm\avg{v_x^2}. \end{equation} Did we forget to include the factor $2$? No; of all the atoms, only half are headed toward the piston. The other half are headed the other way, so the number of atoms per unit volume that are hitting the piston is only $n/2$.
Now as the atoms bounce around, it is clear that there is nothing special about the “$x$-direction”; the atoms may also be moving up and down, back and forth, in and out. Therefore it is going to be true that $\avg{v_x^2}$, the average motion of the atoms in one direction, and the average in the other two directions, are all going to be equal: \begin{equation} \label{Eq:I:39:6} \avg{v_x^2} = \avg{v_y^2} = \avg{v_z^2}. \end{equation} It is only a matter of rather tricky mathematics to notice, therefore, that they are each equal to one-third of their sum, which is of course the square of the magnitude of the velocity: \begin{equation} \label{Eq:I:39:7} \avg{v_x^2} = \tfrac{1}{3}\avg{v_x^2 + v_y^2 + v_z^2} = \avg{v^2}/3. \end{equation} This has the advantage that we do not have to worry about any particular direction, and so we write our pressure formula again in this form: \begin{equation} \label{Eq:I:39:8} P = (\tfrac{2}{3})n\avg{mv^2/2}. \end{equation} The reason we wrote the last factor as $\avg{mv^2/2}$ is that this is the kinetic energy of the center-of-mass motion of the molecule. We find, therefore, that \begin{equation} \label{Eq:I:39:9} PV = N(\tfrac{2}{3})\avg{mv^2/2}. \end{equation} With this equation we can calculate how much the pressure is, if we know the speeds.
As a very simple example let us take helium gas, or any other gas, like mercury vapor, or potassium vapor of high enough temperature, or argon, in which all the molecules are single atoms, for which we may suppose that there is no internal motion in the atom. If we had a complex molecule, there might be some internal motion, mutual vibrations, or something. We suppose that we may disregard that; this is actually a serious matter that we will have to come back to, but it turns out to be all right. We suppose that the internal motion of the atoms can be disregarded, and therefore, for this purpose, that the kinetic energy of the center-of-mass motion is all the energy there is. So for a monatomic gas, the kinetic energy is the total energy. In general, we are going to call $U$ the total energy (it is sometimes called the total internal energy—we may wonder why, since there is no external energy to a gas), i.e., all the energy of all the molecules in the gas, or the object, whatever it is.
For a monatomic gas we will suppose that the total energy $U$ is equal to a number of atoms times the average kinetic energy of each, because we are disregarding any possibility of excitation or motion inside the atoms themselves. Then, in these circumstances, we would have \begin{equation} \label{Eq:I:39:10} PV = \tfrac{2}{3}U. \end{equation}
Incidentally, we can stop here and find the answer to the following question: Suppose that we take a can of gas and compress the gas slowly, how much pressure do we need to squeeze the volume down? It is easy to find out, since the pressure is $\tfrac{2}{3}$ the energy divided by $V$. As we squeeze it down, we do work on the gas and we thereby increase the energy $U$. So we are going to have some kind of a differential equation: If we start out in a given circumstance with a certain energy and a certain volume, we then know the pressure. Now we start to squeeze, but the moment we do, the energy $U$ increases and the volume $V$ decreases, so the pressure goes up.
So, we have to solve a differential equation, and we will solve it in a moment. We must first emphasize, however, that as we are compressing this gas, we are supposing that all the work goes into increasing the energy of the atoms inside. We may ask, “Isn’t that necessary? Where else could it go?” It turns out that it can go another place. There are what we call “heat leaks” through the walls: the hot (i.e., fast-moving) atoms that bombard the walls, heat the walls, and energy goes away. We shall suppose for the present that this is not the case.
For somewhat wider generality, although we are still making some very special assumptions about our gas, we shall write, not $PV = \tfrac{2}{3}U$, but \begin{equation} \label{Eq:I:39:11} PV = (\gamma - 1)U. \end{equation} It is written $(\gamma - 1)$ times $U$ for conventional reasons(see lambda), because we will deal with a few other cases later where the number in front of $U$ will not be $\tfrac{2}{3}$, but will be a different number. So, in order to do the thing in general, we call it $\gamma - 1$, because people have been calling it that for almost one hundred years. This $\gamma$, then, is $\tfrac{5}{3}$ for a monatomic gas like helium, because $\tfrac{5}{3} - 1$ is $\tfrac{2}{3}$.
We have already noticed that when we compress a gas the work done is $-P\,dV$. A compression in which there is no heat energy added or removed is called an adiabatic compression, from the Greek a (not) $+$ dia (through) $+$ bainein (to go). (The word adiabatic is used in physics in several ways, and it is sometimes hard to see what is common about them.) That is, for an adiabatic compression all the work done goes into changing the internal energy. That is the key—that there are no other losses of energy—for then we have $P\,dV = -dU$. But since $U = PV/(\gamma - 1)$, we may write \begin{equation} \label{Eq:I:39:12} dU = (P\,dV + V\,dP)/(\gamma - 1). \end{equation} So we have $P\,dV = -(P\,dV + V\,dP)/(\gamma - 1)$, or, rearranging the terms, $\gamma P\,dV = -V\,dP$, or \begin{equation} \label{Eq:I:39:13} (\gamma\,dV/V) + (dP/P) = 0. \end{equation} Fortunately, assuming that $\gamma$ is constant, as it is for a monatomic gas, we can integrate this: it gives $\gamma\ln V + \ln P = \ln C$, where $\ln C$ is the constant of integration. If we take the exponential of both sides, we get the law \begin{equation} \label{Eq:I:39:14} PV^\gamma = C\text{ (a constant)}. \end{equation} In other words, under adiabatic conditions, where the temperature rises as we compress because no heat is being lost, the pressure times the volume to the $\tfrac{5}{3}$ power is a constant for a monatomic gas! Although we derived it theoretically, this is, in fact, the way monatomic gases behave experimentally.
* mono가 아닌 di 등 혼합된 기체 => 섹션 40의 5
2024.1.4: somehow 질량끼리 충돌하는 경우, 순간적으로 질량이 수축하는 과정으로 봐야 한다
물리가 자연을 양적 기술 도구인 수학으로 종이에 기재한 건데, 전자는 3차원이 아닌 높은 차원과 연결되어야 한다 => 세상은 vector bundle, 전자 하나 하나마다에 3차원이 지정된... 그런데 그 전자 요동의 빛은 interactive하다... 낮은 3차원에 project되었다는 건가? 2차원에 3차원의 그림자처럼? blow-up이란 것이 소위 승천인가?
39–3Compressibility of radiation
We may give one other example of the kinetic theory of a gas, one which is not used in chemistry so much, but is used in astronomy. We have a large number of photons in a box in which the temperature is very high. (The box is, of course, the gas in a very hot star. The sun is not hot enough; there are still too many atoms, but at still higher temperatures in certain very hot stars, we may neglect the atoms and suppose that the only objects that we have in the box are photons.) Now then, a photon has a certain momentum $\FLPp$. (We always find that we are in terrible trouble when we do kinetic theory: $p$ is the pressure, but $p$ is the momentum; $v$ is the volume, but $v$ is the velocity; $T$ is the temperature, but $T$ is the kinetic energy or the time or the torque; one must keep one’s wits about one!) This $\FLPp$ is momentum, it is a vector. Going through the same analysis as before, it is the $x$-component of the vector $\FLPp$ which generates the “kick,” and twice the $x$-component of the vector $\FLPp$ is the momentum which is given in the kick. Thus $2p_x$ replaces $2mv_x$, and in evaluating the number of collisions, $v_x$ is still $v_x$, so when we get all the way through, we find that the pressure in Eq. (39.4) is, instead, \begin{equation} \label{Eq:I:39:15} P = 2np_xv_x. \end{equation} Then, in the averaging, it becomes $n$ times the average of $p_xv_x$ (the same factor of $2$) and, finally, putting in the other two directions, we find \begin{equation} \label{Eq:I:39:16} PV = N\avg{\FLPp\cdot\FLPv}/3. \end{equation} This checks with the formula (39.9), because the momentum is $m\FLPv$; it is a little more general, that is all. The pressure times the volume is the total number of atoms times $\tfrac{1}{3}(\FLPp\cdot\FLPv)$, averaged.
Now, for photons, what is $\FLPp\cdot\FLPv$? The momentum and the velocity are in the same direction, and the velocity is the speed of light, so this is the momentum of each of the objects, times the speed of light. The momentum times the speed of light of every photon is its energy: $E = pc$, so these terms are the energies of each of the photons, and we should, of course, take an average energy, times the number of photons. So we have $\tfrac{1}{3}$ of the energy inside the gas: \begin{equation} \label{Eq:I:39:17} PV = U/3\text{ (photon gas)}. \end{equation} For photons, then, since we have $\tfrac{1}{3}$ in front, $(\gamma - 1)$ in (39.11) is $\tfrac{1}{3}$, or $\gamma = \tfrac{4}{3}$, and we have discovered that radiation in a box obeys the law \begin{equation} \label{Eq:I:39:18} PV^{4/3} = C. \end{equation} So we know the compressibility of radiation! That is what is used in an analysis of the contribution of radiation pressure in a star, that is how we calculate it, and how it changes when we compress it. What wonderful things are already within our power!
39–4Temperature and kinetic energy
So far we have not dealt with temperature; we have purposely been avoiding the temperature. As we compress a gas, we know that the energy of the molecules increases, and we are used to saying that the gas gets hotter; we would like to understand what this has to do with the temperature. If we try to do the experiment, not adiabatically but at what we call constant temperature, what are we doing? We know that if we take two boxes of gas and let them sit next to each other long enough, even if at the start they were at what we call different temperatures, they will in the end come to the same temperature. Now what does that mean? That means that they get to a condition that they would get to if we left them alone long enough! What we mean by equal temperature is just that—the final condition when things have been sitting around interacting with each other long enough.
Let us consider, now, what happens if we have two gases in containers separated by a movable piston as in Fig. 39–2 (just for simplicity we shall take two monatomic gases, say helium and neon). In container (1) the atoms have mass $m_1$, velocity $v_1$, and there are $n_1$ per unit volume, and in the other container the atoms have mass $m_2$, velocity $v_2$, there are $n_2$ atoms per unit volume. What are the conditions for equilibrium?
Obviously, the bombardment from the left side must be such that it moves the piston to the right and compresses the other gas until its pressure builds up, and the thing will thus slosh back and forth, and will gradually come to rest at a place where the pressures are equal on both sides. So we can arrange that the pressures are equal; that just means that the internal energies per unit volume are equal, or that the numbers $n$ times the average kinetic energies on each side are equal. What we have to try to prove, eventually, is that the numbers themselves are equal. So far, all we know is that the numbers times the kinetic energies are equal, \begin{equation*} n_1\avg{m_1v_1^2/2} = n_2\avg{m_2v_2^2/2}, \end{equation*} from (39.8), because the pressures are equal. We must realize that this is not the only condition over the long run, but something else must happen more slowly as the true complete equilibrium corresponding to equal temperatures sets in.
To see the idea, suppose that the pressure on the left side were developed by having a very high density but a low velocity. By having a large $n$ and a small $v$, we can get the same pressure as by having a small $n$ and a large $v$. The atoms may be moving slowly but be packed nearly solidly, or there may be fewer but they are hitting harder. Will it stay like that forever? At first we might think so, but then we think again and find we have forgotten one important point. That is, that the intermediate piston does not receive a steady pressure; it wiggles, just like the eardrum that we were first talking about, because the bangings are not absolutely uniform. There is not a perpetual, steady pressure, but a tattoo—the pressure varies, and so the thing jiggles. Suppose that the atoms on the right side are not jiggling much, but those on the left are few and far between and very energetic. The piston will, now and then, get a big impulse from the left, and will be driven against the slow atoms on the right, giving them more speed. (As each atom collides with the piston, it either gains or loses energy, depending upon whether the piston is moving one way or the other when the atom strikes it.) So, as a result of the collisions, the piston finds itself jiggling, jiggling, jiggling, and this shakes the other gas—it gives energy to the other atoms, and they build up faster motions, until they balance the jiggling that the piston is giving to them. The system comes to some equilibrium where the piston is moving at such a mean square speed that it picks up energy from the atoms at about the same rate as it puts energy back into them. So the piston picks up a certain mean irregularity in speed, and it is our problem to find it. When we do find it, we can solve our problem better, because the gases will adjust their velocities until the rate at which they are trying to pour energy into each other through the piston will become equal.
2023.1.15: 항상 에너지 큰 쪽에서 작은 쪽으로 전달되는 건 아니다, 1차원 예들
1. $m_1=100, v_1=10, m_2=90, 10< v_2 <\frac{10}3 \sqrt{10}$ 경우,
$ m_2 v_2^2 < 90\times \frac{10000}{9}=m_1v_1^2$. 속도가 빠른 $m_2$가 뒤에서 $m_1$을 치받으며 에너지 전달.
2. 서로 치받는 $m_1=m, m_2=2m, v_1=v, v_2=-v$ 경우
$v_{\text{CM}}=-\frac{v}3, u_1=-(v-v_{\text{CM}})=-\frac{4v}3, u_2=(--v-(-\frac{v}3))=\frac{2v}3$. 여기서 by adding $v_{\text{CM}}$, 리바운드 속도는 각각
$-\frac{5}{3}v, \, \frac13v$ 에너지가 $m_2$에서 $m_1$으로 옮겨감.
It is quite difficult to figure out the details of the piston in this particular circumstance; although it is ideally simple to understand, it turns out to be a little harder to analyze. Before we analyze that, let us analyze another problem in which we have a box of gas but now we have two different kinds of molecules in it, having masses $m_1$ and $m_2$, velocities $v_1$ and $v_2$, and so forth; there is now a much more intimate relationship. If all of the No. $2$ molecules are standing still, that condition is not going to last, because they get kicked by the No. $1$ molecules and so pick up speed. If they are all going much faster than the No. $1$ molecules, then maybe that will not last either—they will pass the energy back to the No. $1$ molecules. So when both gases are in the same box, the problem is to find the rule that determines the relative speeds of the two.
This is still a very difficult problem, but we will solve it as follows. First we consider the following sub-problem (again this is one of those cases where—never mind the derivation—in the end the result is very simple to remember, but the derivation is just ingenious). Let us suppose that we have two molecules, of different mass, colliding, and that the collision is viewed in the center-of-mass (CM) system. In order to remove a complication, we look at the collision in the CM. As we know from the laws of collision, by the conservation of momentum and energy, after the molecules collide the only way they can move is such that each maintains its own original speed—and they just change their direction. So we have an average collision that looks like that in Fig. 39–3.
2023.1.8: 헷갈릴 수 있는 노테이션부터 확실히. 먼저
질량 ($m_1, m_2$) 속도는 각각: 충돌 전 ($v_1, v_2$), 후는 ($u_1, u_2$)라고 하자.
1. 운동량 보전 법칙에 의해,
$m_1v_1+m_2v_2=m_1 u_1+m_2 u_2,\, v_{\text{CM}}=u_{\text{CM}}.$ 질량중심 좌표계에서의 속도는 각각
$v_1-v_{\text{CM}}=\frac{m_2}{m_1+m_2}(v_1-v_2), \,
v_2-v_{\text{CM}}=-\frac{m_1}{m_1+m_2}(v_1-v_2)$
$u_1-u_{\text{CM}}=\frac{m_2}{m_1+m_2}(u_1-u_2), \,
u_2-u_{\text{CM}}=-\frac{m_1}{m_1+m_2}(u_1-u_2)$
여기서 주목해야 할 것: 질량 $m_1$과 $m_2$의 충돌 전후 속도들이 같은 방향으로 부호만 다르다는 거.
2. 계산 단순화를 위해, $e_1, e_2$를 질량중심계의 서로 수직인 기본 벡터라하고
$v_1-v_{\text{CM}}=a e_1,\, v_2-v_{\text{CM}}= b e_1$ 하면,
$u_1-u_{\text{CM}}=c e_1+ d e_2,\, u_2-u_{\text{CM}}= f e_1+ g e_2$로 표시될 수 있고,
① 위 주목으로부터 $\frac{d}{c}=\frac{g}{f}=k$, 기울기. 미지수는 $c, d, f, g$
② 질량중심계 원점, $\frac{m_1 ae_1+m_2 be_1}{m_1+m_2}=0$
여기에 질량중심계에서의 운동량 보존을 적용하면,
$0= m_1(a e_1)+m_2(b e_1)=m_1(c e_1+ d e_2)+m_2(f e_1+ g e_2)$ =>
$m_1d+m_2g=0, \, m_1c+m_2f=0$
let $m=\frac{m_1}{m_2}$. 정리하면 $m=-\frac gd = -\frac{f}{c}=-\frac{b}{a}, \,d=ck,\, g=fk$
3. elastic 에너지 보존식, $m_1a^2+m_2 b^2=m_1(c^2+d^2)+m_2(f^2+g^2)$의 양변을 $m_2$로 나누고
$b=am, d=ck, f=ck, f=-cm$ 대입하면,
$ma^2+a^2m^2=m(c^2+c^2k^2)+(f^2+f^2k^2)$
$a^2(m+m^2)=mc^2(1+k^2)+f^2(1+k^2)=mc^2(1+k^2)+c^2m^2(1+k^2)=c^2(m+m^2)(1+k^2)$
$a^2=c^2(1+k^2)=c^2+d^2$, which implies $|ae_1|=|u_1-u_{\text{CM}}=c e_1+ d e_2|$ => 충돌 입자의 속력은 튕겨나갈 때와 같다, 즉 only change their direction
They are equally likely to go in all directions, but how do we say that? There is of course no likelihood that they will go in any specific direction, because a specific direction is too exact, so we have to talk about per unit “something.” The idea is that any area on a sphere centered at a collision point will have just as many molecules going through it as go through any other equal area on the sphere. So the result of the collisions will be to distribute the directions so that equal areas on a sphere will have equal probabilities.
Incidentally, if we just want to discuss the original direction and some other direction an angle $\theta$ from it, it is an interesting property that the differential area of a sphere of unit radius is $\sin\theta\,d\theta$ times $2\pi$ (see Fig. 32–1). And $\sin\theta\,d\theta$ is the same as the differential of $-\cos\theta$. So what it means is that the cosine of the angle $\theta$ between any two directions is equally likely to be anything from $-1$ to $+1$.
2021(전에 했던 날짜 모름)
$
\frac{1}{4\pi}\, \lim_{\Delta\theta\rightarrow 0}{\sum_{\theta=0}^{\pi}} \cos\theta 2\pi \Delta\theta= \frac{1}{4\pi}\
\lim_{\Delta\theta\rightarrow 0}{\sum_{\theta=0}^{\pi}}\sin\theta\, 2\pi d\theta=-\frac{1}{2}\int_{\cos{\theta}=1}^{-1}d\cos\theta
=\frac{1}{2}\cos\theta \rvert_{-1}^{1}=1$.
여기서 $4\pi=단위구\,면적$
Next, we have to worry about the actual case, where we do not have the collision in the CM system, but we have two atoms which are coming together with vector velocities $\FLPv_1$ and $\FLPv_2$. What happens now? We can analyze this collision with the vector velocities $\FLPv_1$ and $\FLPv_2$ in the following way: We first say that there is a certain CM; the velocity of the CM is given by the “average” velocity, with weights proportional to the masses, so the velocity of the CM is $\FLPv_{\text{CM}} =(m_1\FLPv_1 + m_2\FLPv_2)/(m_1 + m_2)$. If we watch this collision in the CM system, then we see a collision just like that in Fig. 39–3, with a certain relative velocity $\FLPw$ coming in. The relative velocity is just $\FLPv_1 - \FLPv_2$. Now the idea is that, first, the whole CM is moving, and in the CM there is a relative velocity $\FLPw$, and the molecules collide and come off in some new direction. All this happens while the CM keeps right on moving, without any change.
22.3.14: No 충돌 case => pick 충돌하는 2 원자들 with $v_1, v_2$ => 그리고 위에서 전개한 논리를 여기에 적용. 문제는 두번째 단계의 원자들 존재 문제
$\int =\sum$로 취급하고, 평균, 근사값 다루는데 익숙한 물리학자와 달리 수학자는 받아들이는 게 쉽지 않다.
똑 떨어지게 맞는 것들이 존재하지 않을 수 있지만, 평형상태의 수많은 충돌 원자들 속에는 주어진 속도들에 아주 근접한 것들이 존재한다, 무리수에 원하는 만큼에 거리내의 유리수 찾을 수 있듯이. 게다가 증명할 식(39.19)도 precisely equal이 아니다. 물리는 인간 관측 한계내 학문이니, 평형상태에서 수학적으로 equal 취급하는 거.
* 좀 더 제대로된 설명, 아래
2023.1.13: 임의의 2 개스 분자의 relative 속도 분포 분석
(1) 충돌 경우
(2) 엇갈리는 경우
① '더' CM system과 '어' CM을 혼동하지 말도록
② 극한 상황 적용
2023.1.26: Which atom gain energy while the other loses ?
아래 그림: 구의 중심은 질량 중심 벡터 $v_M$의 끝점, $Q$이고 반지름은 $|v_1-v_M|$. $|v_1-v_M|=|u_1|, |v_2-v_M|=|u_2|$, $C$는 $Q$를 꼭지로 $QP, u_1$이 만드는 원뿔의 바닥원.
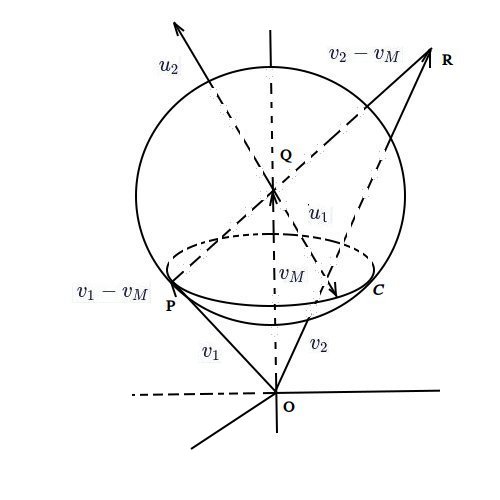
$m_1$이 충돌 후 튕겨지는 속도 범위는 구 표면. 속력 $|v_M+u_1|$은 $u_1$이 $C$위에 있을 때 $|v_1|$과 같고 그 바깥쪽은 크고 안쪽은 작아진다. 이 그림의 경우, $m_1$이 에너지 얻을 확률이 많다, 물론 평형상태 가정에서.
Now then, what is the distribution resulting from this? From our previous argument we conclude this: that at equilibrium, all directions for $\FLPw$ are equally likely, relative to the direction of the motion of the CM.1 There will be no particular correlation, in the end, between the direction of the motion of the relative velocity and that of the motion of the CM. Of course, if there were, the collisions would spray it about, so it is all sprayed around. So the cosine of the angle between $\FLPw$ and $\FLPv_{\text{CM}}$ is zero on the average(* 맥스웰 업적). That is, \begin{equation} \label{Eq:I:39:19} \avg{\FLPw\cdot\FLPv_{\text{CM}}} = 0. \end{equation} But $\FLPw\cdot\FLPv_{\text{CM}}$ can be expressed in terms of $\FLPv_1$ and $\FLPv_2$ as well: \begin{align} \FLPw\cdot\FLPv_{\text{CM}} &= \frac{(\FLPv_1 - \FLPv_2)\cdot(m_1\FLPv_1 + m_2\FLPv_2)} {m_1 + m_2}\notag\\[1.5ex] \label{Eq:I:39:20} &= \frac{(m_1v_1^2 - m_2v_2^2) + (m_2 - m_1)(\FLPv_1\cdot\FLPv_2)} {m_1 + m_2}. \end{align}
First, let us look at the $\FLPv_1\cdot\FLPv_2$; what is the average of $\FLPv_1\cdot\FLPv_2$? That is, what is the average of the component of velocity of one molecule in the direction of another? Surely there is just as much likelihood of finding any given molecule moving one way as another. The average of the velocity $\FLPv_2$ in any direction is zero. Certainly, then, in the direction of $\FLPv_1$, $\FLPv_2$ has zero average. So, the average of $\FLPv_1\cdot\FLPv_2$ is zero! Therefore, we conclude that the average of $m_1v_1^2$ must be equal to the average of $m_2v_2^2$. That is, the average kinetic energy of the two must be equal: \begin{equation} \label{Eq:I:39:21} \avg{\tfrac{1}{2}m_1v_1^2} = \avg{\tfrac{1}{2}m_2v_2^2}. \end{equation} If we have two kinds of atoms in a gas, it can be shown, and we presume to have shown it
(* 실험상 미리 알고 입증. 21.7.9 보충: 이쯤에서 '에너지'라는 것이 온도라는 것을 인식했어야... 온도가 같아지는 평형상태라는 것은 결국 2기체 분자들이 충돌하며 주고 받는 운동 에너지가 같다는 거 아이가 말이다. 물리란 현상을 제대로 봐야 한다. 가정에서 출발하여 그에 따른 결과를 유도하는 수학과 달리, 물리는 현상에서 가정을 끌어내는 것이기에.)
, that the average of the kinetic energy of one is the same as the average of the kinetic energy of the other, when they are both in the same gas in the same box in equilibrium. That means that the heavy ones will move slower than the light ones; this is easily shown by experimentation with “atoms” of different masses in an air trough.Now we would like to go one step further, and say that if we have two different gases separated in a box, they will also have equal average kinetic energy when they have finally come to equilibrium, even though they are not in the same box. We can make the argument in a number of ways. One way is to argue that if we have a fixed partition with a tiny hole in it (Fig. 39–4) so that one gas could leak out through the holes while the other could not, because the molecules are too big, and these had attained equilibrium, then we know that in one part, where they are mixed, they have the same average kinetic energy, but some come through the hole without loss of kinetic energy, so the average kinetic energy in the pure gas and in the mixture must be the same. That is not too satisfactory, because maybe there are no holes, for this kind of molecule, that separate one kind from the other.
Let us now go back to the piston problem. We can give an argument which shows that the kinetic energy of this piston must also be $\tfrac{1}{2}m_2v_2^2$. Actually, that would be the kinetic energy due to the purely horizontal motion of the piston, so, forgetting its up and down motion, it will have to be the same as $\tfrac{1}{2}m_2v_{2_x}^2$. Likewise, from the equilibrium on the other side, we can prove that the kinetic energy of the piston is $\tfrac{1}{2}m_1v_{1_x}^2$. Although this is not in the middle of the gas, but is on one side of the gas, we can still make the argument, although it is a little more difficult, that the average kinetic energy of the piston and of the gas molecules are equal as a result of all the collisions.
* 위에서 언급한 the cosine of the angle between $\FLPw$
and $\FLPv_{\text{CM}}$ is zero on the average인 경우,
$\avg{\FLPw\cdot\FLPv_{\text{CM}}}=0 \Leftrightarrow <|w||v_{\text{CM}}|><\cos{\theta}>$, 여기서 $<\cos{\theta}>=\frac{1}{2\pi}\int_0^{2\pi}\cos{\theta} d{\theta}=0$
'not in the middle of the gas, but is on one side of the gas'인 경우는
$<\cos{\theta}>=\frac{1}{\pi}\int_{\delta}^{\pi+\delta}\cos{\theta}d{\theta}$이고 여전히 0
If this still does not satisfy us, we may make an artificial example by which the equilibrium is generated by an object which can be hit on all sides. Suppose that we have a short rod with a ball on each end sticking through the piston, on a frictionless sliding universal joint. Each ball is round, like one of the molecules, and can be hit on all sides. This whole object has a certain total mass, $m$. Now, we have the gas molecules with mass $m_1$ and mass $m_2$ as before. The result of the collisions, by the analysis that was made before, is that the kinetic energy of $m$ because of collisions with the molecules on one side must be $\tfrac{1}{2}m_1v_1^2$, on the average. Likewise, because of the collisions with molecules on the other side, it has to be $\tfrac{1}{2}m_2v_2^2$ on the average. So, therefore, both sides have to have the same kinetic energy when they are in thermal equilibrium. So, although we only proved it for a mixture of gases, it is easily extended to the case where there are two different, separate gases at the same temperature.
Thus when we have two gases at the same temperature, the mean kinetic energy of the CM motions are equal.
The mean molecular kinetic energy is a property only of the “temperature.” Being a property of the “temperature,” and not of the gas, we can use it as a definition of the temperature. The mean kinetic energy of a molecule is thus some function of the temperature. But who is to tell us what scale to use for the temperature? We may arbitrarily define the scale of temperature so that the mean energy is linearly proportional to the temperature. The best way to do it would be to call the mean energy itself “the temperature.” That would be the simplest possible function. Unfortunately, the scale of temperature has been chosen differently, so instead of calling it temperature directly we use a constant conversion factor between the energy of a molecule and a degree of absolute temperature called a degree Kelvin. The constant of proportionality is $k = 1.38\times10^{-23}$ joule for every degree Kelvin.2 So if $T$ is absolute temperature, our definition says that the mean molecular kinetic energy is $\tfrac{3}{2}kT$. (The $\tfrac{3}{2}$ is put in as a matter of convenience, so as to get rid of it somewhere else.)
2021.3.31: 에너지와 온도가 equivalent하다는 것 => 열/에너지= 진동수=온도
We point out that the kinetic energy associated with the component of motion in any particular direction is only $\tfrac{1}{2}kT$. The three independent directions that are involved make it $\tfrac{3}{2}kT$.
39–5The ideal gas law
Now, of course, we can put our definition of temperature into Eq. (39.9) and so find the law for the pressure of gases as a function of the temperature: it is that the pressure times the volume is equal to the total number of atoms times the universal constant $k$, times the temperature: \begin{equation} \label{Eq:I:39:22} PV = NkT. \end{equation} Furthermore, at the same temperature and pressure and volume, the number of atoms is determined; it too is a universal constant! So equal volumes of different gases, at the same pressure and temperature, have the same number of molecules, because of Newton’s laws. That is an amazing conclusion!
In practice, when dealing with molecules, because the numbers are so large, the chemists have artificially chosen a specific number, a very large number, and called it something else. They have a number which they call a mole. A mole is merely a handy number. Why they did not choose $10^{24}$ objects, so it would come out even, is a historical question. They happened to choose, for the convenient number of objects on which they standardize, $N_0 = 6.02\times10^{23}$ objects, and this is called a mole of objects. So instead of measuring the number of molecules in units, they measure in terms of numbers of moles.3 In terms of $N_0$ we can write the number of moles, times the number of atoms in a mole, times $kT$, and if we want to, we can take the number of atoms in a mole times $k$, which is a mole’s worth of $k$, and call it something else, and we do—we call it $R$. A mole’s worth of $k$ is $8.317$ joules: $R = N_0k = 8.317$ J${}\cdot{}$mole$^{-1}\cdot{}^\circ$K$^{-1}$. Thus we also find the gas law written as the number of moles (also called $N$) times $RT$, or the number of atoms, times $kT$: \begin{equation} \label{Eq:I:39:23} PV = NRT. \end{equation} It is the same thing, just a different scale for measuring numbers. We use $1$ as a unit, and chemists use $6\times10^{23}$ as a unit!
We now make one more remark about our gas law, and that has to do with the law for objects other than monatomic molecules. We have dealt only with the CM motion of the atoms of a monatomic gas. What happens if there are forces present? First, consider the case that the piston is held by a horizontal spring, and there are forces on it. The exchange of jiggling motion between atoms and piston at any moment does not depend on where the piston is at that moment(See for each $x$.), of course. The equilibrium conditions are the same. No matter where the piston is, its speed of motion must be such that it passes energy to the molecules in just the right way. So it makes no difference about the spring. The speed at which the piston has to move, on the average, is the same.
2024.4.24: 구조보존 법칙과 마찬가지로 평형상태를 가정했으니, 모든 건 평형상태가 이루어지도록 움직여야 한다는 restriction이 있다는 거.
그 restriction은 왔다갔다하는 움직임, 즉 에너지 $\frac12 m{v}^2$가 같아야 하는 거니 속도가 같을 수 밖에
2023.2.2: The answer is .... a certain important
assumption, which is that if a given system is in thermal equilibrium
at some temperature, it will also be in thermal equilibrium with
anything else
2.22: 움직임을 전달하는 전달체의 운동에 무관한 파동 방정식
2024.4.21: 스프링으로 연결된 2 진자의 움직임 교환. 신경 거슬리는 용수철의 움직임은 작용-반작용, 서로간의 영향 등으로 상쇄되고 이동하는 움직임만 남는다.
Consider, for example, a diatomic molecule composed of atoms $m_A$ and $m_B$. What we have proved is that the motion of the CM of part $A$ and that of part $B$ are such that $\avg{\tfrac{1}{2}m_Av_A^2} = \avg{\tfrac{1}{2}m_Bv_B^2} = \tfrac{3}{2}kT$. How can this be, if they are held together? Although they are held together, when they are spinning and turning in there, when something hits them, exchanging energy with them, the only thing that counts is how fast they are moving. That alone determines how fast they exchange energy in collisions. At the particular instant, the force is not an essential point. Therefore the same principle is right, even when there are forces.
Let us prove, finally, that the gas law is consistent also with a disregard of the internal motion. We did not really include the internal motions before; we just treated a monatomic gas. But we shall now show that an entire object, considered as a single body of total mass $M$, has a velocity of the CM such that \begin{equation} \label{Eq:I:39:24} \left\langle\tfrac{1}{2}Mv_{\text{CM}}^2\right\rangle = \tfrac{3}{2}kT. \end{equation} In other words, we can consider either the separate pieces or the whole thing! Let us see the reason for that: The mass of the diatomic molecule is $M = m_A + m_B$, and the velocity of the center of mass is equal to $\FLPv_{\text{CM}} = (m_A\FLPv_A + m_B\FLPv_B)/M$. Now we need $\avg{v_{\text{CM}}^2}$. If we square $\FLPv_{\text{CM}}$, we get \begin{equation*} v_{\text{CM}}^2 = \frac{m_A^2v_A^2 + 2m_Am_B\FLPv_A\cdot\FLPv_B + m_B^2v_B^2}{M^2}. \end{equation*}
Now we multiply $\tfrac{1}{2}M$ and take the average, and thus we get \begin{align*} \left\langle\tfrac{1}{2}Mv_{\text{CM}}^2\right\rangle &= \frac{m_A\tfrac{3}{2}kT + m_Am_B\avg{\FLPv_A\cdot\FLPv_B} + m_B\tfrac{3}{2}kT}{M}\\[.5ex] &= \tfrac{3}{2}kT + \frac{m_Am_B\avg{\FLPv_A\cdot\FLPv_B}}{M}. \end{align*} (We have used the fact that $(m_A + m_B)/M = 1$.) Now what is $\avg{\FLPv_A\cdot\FLPv_B}$? (It had better be zero!) To find out, let us use our assumption that the relative velocity, $\FLPw = \FLPv_A - \FLPv_B$ is not any more likely to point in one direction than in another—that is, that its average component in any direction is zero. Thus we assume that \begin{equation*} \avg{\FLPw\cdot\FLPv_{\text{CM}}} = 0. \end{equation*} But what is $\FLPw\cdot\FLPv_{\text{CM}}$? It is \begin{align*} \FLPw\cdot\FLPv_{\text{CM}} &= \frac{(\FLPv_A - \FLPv_B)\cdot (m_A\FLPv_A + m_B\FLPv_B)}{M}\\[.5ex] &= \frac{m_Av_A^2 + (m_B - m_A)(\FLPv_A\cdot\FLPv_B) - m_Bv_B^2}{M}. \end{align*} Therefore, since $\avg{m_Av_A^2} = \avg{m_Bv_B^2}$, the first and last terms cancel out on the average, and we are left with \begin{equation*} (m_B - m_A)\avg{\FLPv_A\cdot\FLPv_B} = 0. \end{equation*} Thus if $m_A \neq m_B$, we find that $\avg{\FLPv_A\cdot\FLPv_B} = 0$, and therefore that the bodily motion of the entire molecule, regarded as a single particle of mass $M$, has a kinetic energy, on the average, equal to $\tfrac{3}{2}kT$.
Incidentally, we have also proved at the same time that the average kinetic energy of the internal motions of the diatomic molecule, disregarding the bodily motion of the CM, is $\tfrac{3}{2}kT$! For, the total kinetic energy of the parts of the molecule is $\tfrac{1}{2}m_Av_A^2 + \tfrac{1}{2}m_Bv_B^2$, whose average is $\tfrac{3}{2}kT + \tfrac{3}{2}kT$, or $3kT$. The kinetic energy of the center-of-mass motion is $\tfrac{3}{2}kT$, so the average kinetic energy of the rotational and vibratory motions of the two atoms inside the molecule is the difference, $\tfrac{3}{2}kT$.
The theorem concerning the average energy of the CM motion is general: for any object considered as a whole, with forces present or no, for every independent direction of motion that there is, the average kinetic energy in that motion is $\tfrac{1}{2}kT$.
* n 질량의 CM system은 두개 질량의 CM system의 iteration 결과
$\FLPv_{\text{CM_n}} = (\sum_{i=0}^nm_i\FLPv_i)/{\sum_{i=0}^n{m_i}}$ 라고 하면, $\FLPv_{\text{CM_{n+1}}}=\frac{({\sum_{i=0}^n{m_i}})\FLPv_{\text{CM_n}}+m_{n+1}v_{n+1}}{\sum_{i=0}^{n+1}m_i}$
따라서, 모든 물질의 질량중심의 평균 kinetic 에너지는 $\frac32kT$
The latter can sometimes be expressed as a sum of rotational kinetic energy of the molecule and vibrational energy, but this is an approximation. Our theorem, applied to the $r$-atom molecule, says that the molecule will have, on the average, $3rkT/2$ joules of kinetic energy, of which $\tfrac{3}{2}kT$ is kinetic energy of the center-of-mass motion of the entire molecule, and the rest, $\tfrac{3}{2}(r - 1)kT$, is internal vibrational and rotational kinetic energy.
- This argument, which was the one used by Maxwell, involves some subtleties. Although the conclusion is correct, the result does not follow purely from the considerations of symmetry that we used before, since, by going to a reference frame moving through the gas, we may find a distorted velocity distribution. We have not found a simple proof of this result. ↩
- The centigrade scale is just this Kelvin scale with a zero chosen at $273.15$ $^\circ$K, so $T = 273.15 + \text{centigrade temperature}$. ↩
- What the chemists call molecular weights are the masses in grams of a mole of a molecule. The mole is defined so that the mass of a mole of carbon atoms of isotope $12$ (i.e., having $6$ protons and $6$ neutrons in the nucleus) is exactly $12$ grams. ↩