46 Ratchet and pawl1
Ratchet and pawl1
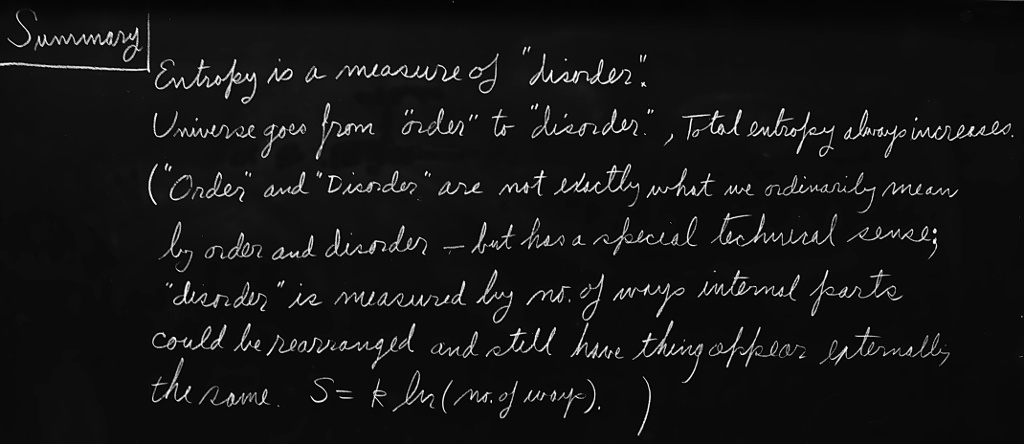
46–1How a ratchet works
In this chapter we discuss the ratchet and pawl, a very simple device which allows a shaft to turn only one way. The possibility of having something turn only one way requires some detailed and careful analysis, and there are some very interesting consequences.
The plan of the discussion came about in attempting to devise an elementary explanation, from the molecular or kinetic point of view, for the fact that there is a maximum amount of work which can be extracted from a heat engine. Of course we have seen the essence of Carnot’s argument, but it would be nice to find an explanation which is elementary in the sense that we can see what is happening physically. Now, there are complicated mathematical demonstrations which follow from Newton’s laws to demonstrate that we can get only a certain amount of work out when heat flows from one place to another, but there is great difficulty in converting this into an elementary demonstration. In short, we do not understand it, although we can follow the mathematics.
In Carnot’s argument, the fact that more than a certain amount of work cannot be extracted in going from one temperature to another is deduced from another axiom, which is that if everything is at the same temperature, heat cannot be converted to work by means of a cyclic process. First, let us back up and try to see, in at least one elementary example, why this simpler statement is true.
Let us try to invent a device which will violate the Second Law of Thermodynamics, that is, a gadget which will generate work from a heat reservoir with everything at the same temperature. Let us say we have a box of gas at a certain temperature, and inside there is an axle with vanes in it. (See Fig. 46–1 but take $T_1 =$ $T_2 =$ $T$, say.) Because of the bombardments of gas molecules on the vane, the vane oscillates and jiggles. All we have to do is to hook onto the other end of the axle a wheel which can turn only one way—the ratchet and pawl. Then when the shaft tries to jiggle one way, it will not turn, and when it jiggles the other, it will turn. Then the wheel will slowly turn, and perhaps we might even tie a flea onto a string hanging from a drum on the shaft, and lift the flea! Now let us ask if this is possible. According to Carnot’s hypothesis, it is impossible. But if we just look at it, we see, prima facie, that it seems quite possible. So we must look more closely. Indeed, if we look at the ratchet and pawl, we see a number of complications.
First, our idealized ratchet is as simple as possible, but even so, there is a pawl, and there must be a spring in the pawl. The pawl must return after coming off a tooth, so the spring is necessary.
Another feature of this ratchet and pawl, not shown in the figure, is quite essential. Suppose the device were made of perfectly elastic parts. After the pawl is lifted off the end of the tooth and is pushed back by the spring, it will bounce against the wheel and continue to bounce. Then, when another fluctuation came, the wheel could turn the other way, because the tooth could get underneath during the moment when the pawl was up! Therefore an essential part of the irreversibility of our wheel is a damping or deadening mechanism which stops the bouncing. When the damping happens, of course, the energy that was in the pawl goes into the wheel and shows up as heat. So, as it turns, the wheel will get hotter and hotter. To make the thing simpler, we can put a gas around the wheel to take up some of the heat. Anyway, let us say the gas keeps rising in temperature, along with the wheel. Will it go on forever? No! The pawl and wheel, both at some temperature $T$, also have Brownian motion. This motion is such that, every once in a while, by accident, the pawl lifts itself up and over a tooth just at the moment when the Brownian motion on the vanes is trying to turn the axle backwards. And as things get hotter, this happens more often.
So, this is the reason this device does not work in perpetual motion. When the vanes get kicked, sometimes the pawl lifts up and goes over the end. But sometimes, when it tries to turn the other way, the pawl has already lifted due to the fluctuations of the motions on the wheel side, and the wheel goes back the other way! The net result is nothing. It is not hard to demonstrate that when the temperature on both sides is equal, there will be no net average motion of the wheel. Of course the wheel will do a lot of jiggling this way and that way, but it will not do what we would like, which is to turn just one way.
Let us look at the reason. It is necessary to do work against the spring in order to lift the pawl to the top of a tooth. Let us call this energy $\epsilon$, and let $\theta$ be the angle between the teeth. The chance that the system can accumulate enough energy, $\epsilon$, to get the pawl over the top of the tooth, is $e^{-\epsilon/kT}$. But the probability that the pawl will accidentally be up is also $e^{-\epsilon/kT}$. So the number of times that the pawl is up and the wheel can turn backwards freely is equal to the number of times that we have enough energy to turn it forward when the pawl is down. We thus get a “balance,” and the wheel will not go around.
2022.12.6: equilibrium, 평형상태란 서로 주고 받는 게 같다는 건데...
perfect한 평형상태란 이 세상에 없기에. 어딘가는 몰리는 곳이 있고 몰린 곳은 그 크기에 비례하는 영향력을 주변에 행사함으로써 덩치를 불린다. 허지만, 시간이 지나면서 그 몰린 곳 또한 평형상태를 유지할 수 없기에 같은 이유로 분해된다. 나라 등 그 어떤 조직도 통합 분할을 거칠 수 밖에 없는 이유이기도 하고 우주의 별 탄생도 그와 같다, 즉 가스들이 고르게 분포될 수 없고 어딘가 뭉치기에 생긴다는 거.
* 볼쯔만 법칙, $e^{-\epsilon/kT}$
46–2The ratchet as an engine
Let us now go further. Take the example where the temperature of the vanes is $T_1$ and the temperature of the wheel, or ratchet, is $T_2$, and $T_2$ is less than $T_1$. Because the wheel is cold and the fluctuations of the pawl are relatively infrequent, it will be very hard for the pawl to attain an energy $\epsilon$. Because of the high temperature $T_1$, the vanes will often attain the energy $\epsilon$, so our gadget will go in one direction, as designed.
We would now like to see if it can lift weights. Onto the drum in the middle we tie a string, and put a weight, such as our flea, on the string. We let $L$ be the torque due to the weight. If $L$ is not too great, our machine will lift the weight because the Brownian fluctuations make it more likely to move in one direction than the other. We want to find how much weight it can lift, how fast it goes around, and so on.
2022.12.9: 일한다는 건, 운동량이 전달되는 과정 ⇨ 전달하는 축같은 매질 또는 운동량 가진 질량이 직접 충돌-전달하기 위해 구멍 등 통해 목적지 접근
First we consider a forward motion, the usual way one designs a ratchet to run. In order to make one step forward, how much energy has to be borrowed from the vane end? We must borrow an energy $\epsilon$ to lift the pawl. The wheel turns through an angle $\theta$ against a torque $L$, so we also need the energy $L\theta$. The total amount of energy that we have to borrow is thus $\epsilon + L\theta$. The probability that we get this energy is proportional to $e^{-(\epsilon + L\theta)/kT_1}$. Actually, it is not only a question of getting the energy, but we also would like to know the number of times per second it has this energy. The probability per second is proportional to $e^{-(\epsilon + L\theta)/kT_1}$, and we shall call the proportionality constant $1/\tau$. It will cancel out in the end anyway. When a forward step happens, the work done on the weight is $L\theta$. The energy taken from the vane is $\epsilon + L\theta$. The spring gets wound up with energy $\epsilon$, then it goes clatter, clatter, bang, and this energy goes into heat. All the energy taken out goes to lift the weight and to drive the pawl, which then falls back and gives heat to the other side.
Now we look at the opposite case, which is backward motion. What happens here? To get the wheel to go backwards all we have to do is supply the energy to lift the pawl high enough so that the ratchet will slip. This is still energy $\epsilon$. Our probability per second for the pawl to lift this high is now $(1/\tau)e^{-\epsilon/kT_2}$. Our proportionality constant is the same, but this time $kT_2$ shows up because of the different temperature.
2022.12.17: 왜? 비례상수가 같아야 하는지 의문이었는데, 이 chapter에 대한 비판 논문에서도 그에 대해 언급.
When this happens, the work is released because the wheel slips backward. It loses one notch, so it releases work $L\theta$. The energy taken from the ratchet system is $\epsilon$, and the energy given to the gas at $T_1$ on the vane side is $L\theta + \epsilon$. It takes a little thinking to see the reason for that. Suppose the pawl has lifted itself up accidentally by a fluctuation. Then when it falls back and the spring pushes it down against the tooth, there is a force trying to turn the wheel, because the tooth is pushing on an inclined plane. This force is doing work, and so is the force due to the weights. So both together make up the total force, and all the energy which is slowly released appears at the vane end as heat. (Of course it must, by conservation of energy, but one must be careful to think the thing through!)2024.4.24: 움직임이 전달되는 연결된 진자
2022.12.10: 'work on'이란 거
망치로 나무에 못을 박는 과정을 예로 들면, 손이 망치에 망치는 못에 못은 또 나무에 work on 하는 거. '움직임'이 손 ⇨ 망치 ⇨ 못 ⇨ 나무로 전해지는 거(참조: 갈바노미터)
에너지, 힘 무엇이든 간에 움직이도록 만든다는 거야. 못이 나무에 박히지 않아 열이 난다든가 에너지가 열로 상실된다는 거 또한 주변 기체 입자를 움직이게 함으로써 생기는 거.
12.11: force trying to turn
물건 들고 있는 거는 physical work가 아니라 했지만 '움직임'에는 strain도 포함한다는 거...
전에 깨달은 거에 더하여 '움직임'이란 흐름이다. physics란 자연 흐름을 공부하는 거고 흐름은 뭐냐는 건데, 그를 표현하는 에너지, 운동량, 힘 등으로 부족.
'careful to think the thing through!' means '에너지 정의, $\int F \cdot ds$' 개선 필요(* 12.28: 일반화 필요. 에너지는 질량에만 적용된다. 하지만 열은 질량이 없다? 적어도 언급되지 않고 있다. 한의에서 뜸은 활기를 주는 거라 한다. 열=기. 기와 질량 가진 에너지에는 차이가 뭐냐는 건데...
온도 정의 역시 질량들의 운동 에너지로 정의한다. 하여 내부 에너지가 부피와 관계없는 기체를 이상기체 부르고... 각 기체 분자 질량의 활동 영역에 질량이외에 활기없는 기가 차 있고. 질량은 기의 구조물로 활기의 용기로 그 구조물은 활기없는 기로 만들어진 것으로 불투명체와 마찬 가지로 활기들의 합이 서로 상쇄된 거로 보면, zero set. 바다와 육지?)
그리고 reversible이란 그 '움직임'의 흐름 역행이 가능하다는 거.
12.29: careful to think ⇨ virtual work, 이쯤 돼면,
1. 질량은 geometrically structured 기 덩어리
2. 구조 없는 기는 밀도도 없고 질량도 없다, 빛입자 처럼. 그러고 정지한 기는 measure 0, 엔트로피 0
3. 질량이 존재하는 경우, kinetic 에너지. measure 0인 경우 열이나 전자파로 퍼진다, 그러니 활기가 늘어나고 엔트로피가 증가하는 것.
Suppose that for a particular weight the rates happen to be equal. Then we add an infinitesimal weight to the string. The weight will slowly go down, and work will be done on the machine. Energy will be taken from the wheel and given to the vanes. If instead we take off a little bit of weight, then the imbalance is the other way. The weight is lifted, and heat is taken from the vane and put into the wheel.
2022.12.12: 흐름으로 보면, machine은 strained 달리 말하면 pressured 그 '기'는 움직임이 활발해져 옆의 기에게 그 움직임 전달하고 평형 유지.
12.15: 평형, equilibrium은 물질이 fluctuate, 출렁이는 현상
⇨ matter wave, 물질파 ⇨ 카놋과 드 브로이의 missing link?
12.16: 특정 무게에서 평형유지, 시소 또는 양팔 저울처럼 아래위로 흔들리며. 그걸 infinitesimal 무게 변화로 해석한 건데, 무게와 운동량/에너지가 interchangeable하다는 걸 암시.
여하튼 결론은 망치로 못 박는 예로 설명했듯이, '움직임'을 봐야한다.
한쪽의 열저장소(가스들)으로 부터 $Q_1=\epsilon + L\theta$을 얻어 일 시키고 남은 $Q_2=\epsilon$를 다른 가스들에게 내주고 그 역도 성립한다는, 증기기관처럼.
덧붙여, rachet-pawl은 폭포의 물레방아 역행이 생각났는데, 다른 문제임.
| Forward: | Needs energy | $\epsilon + L\theta$ | from vane. $~\therefore\text{ Rate} = \dfrac{1}{\tau}\,e^{-(L\theta +\epsilon)/kT_1}$ |
| Takes from vane | $L\theta + \epsilon$ | ||
| Does work | $L\theta$ | ||
| Gives to ratchet | $\epsilon$ | ||
| Backward: | Needs energy | $\epsilon$ | for pawl. $~\therefore\text{ Rate} = \dfrac{1}{\tau}\,e^{-\epsilon/kT_2}$ |
| Takes from ratchet | $\epsilon$ |
| |
| Releases work | $L\theta$ | ||
| Gives to vane | $L\theta + \epsilon$ |
| If system is reversible, rates are equal, hence $~\dfrac{\epsilon + L\theta}{T_1} = \dfrac{\epsilon}{T_2}$. |
| $\dfrac{\text{Heat to ratchet}}{\text{Heat from vane}} = \dfrac{\epsilon}{L\theta + \epsilon}.~$ Hence $~\dfrac{Q_2}{Q_1} = \dfrac{T_2}{T_1}$. |
Let us now calculate how fast our one-way device would turn if everything were at the same temperature and we hung a weight on the drum. If we pull very, very hard, of course, there are all kinds of complications. The pawl slips over the ratchet, or the spring breaks, or something. But suppose we pull gently enough that everything works nicely. In those circumstances, the above analysis is right for the probability of the wheel going forward and backward, if we remember that the two temperatures are equal. In each step an angle $\theta$ is obtained, so the angular velocity is $\theta$ times the probability of one of these jumps per second. It goes forward with probability $(1/\tau)e^{-(\epsilon + L\theta)/kT}$ and backward with probability $(1/\tau)e^{-\epsilon/kT}$, so that for the angular velocity we have \begin{align} \omega &= (\theta/\tau)(e^{-(\epsilon + L\theta)/kT} - e^{-\epsilon/kT})\notag\\[.5ex] \label{Eq:I:46:1} &= (\theta/\tau)e^{-\epsilon/kT}(e^{-L\theta/kT} - 1). \end{align} If we plot $\omega$ against $L$, we get the curve shown in Fig. 46–2. We see that it makes a great difference whether $L$ is positive or negative. If $L$ increases in the positive range, which happens when we try to drive the wheel backward, the backward velocity approaches a constant. As $L$ becomes negative, $\omega$ really “takes off” forward, since $e$ to a tremendous power is very great!
The angular velocity that was obtained from different forces is thus very unsymmetrical. Going one way it is easy: we get a lot of angular velocity for a little force. Going the other way, we can put on a lot of force, and yet the wheel hardly goes around.
We find the same thing in an electrical rectifier. Instead of the force, we have the electric field, and instead of the angular velocity, we have the electric current. In the case of a rectifier, the voltage is not proportional to resistance, and the situation is unsymmetrical. The same analysis that we made for the mechanical rectifier will also work for an electrical rectifier. In fact, the kind of formula we obtained above is typical of the current-carrying capacities of rectifiers as a function of their voltages.
Now let us take all the weights away, and look at the original machine. If $T_2$ were less than $T_1$, the ratchet would go forward, as anybody would believe. But what is hard to believe, at first sight, is the opposite. If $T_2$ is greater than $T_1$, the ratchet goes around the opposite way! A dynamic ratchet with lots of heat in it runs itself backwards, because the ratchet pawl is bouncing. If the pawl, for a moment, is on the incline somewhere, it pushes the inclined plane sideways. But it is always pushing on an inclined plane, because if it happens to lift up high enough to get past the point of a tooth, then the inclined plane slides by, and it comes down again on an inclined plane. So a hot ratchet and pawl is ideally built to go around in a direction exactly opposite to that for which it was originally designed!
In spite of all our cleverness of lopsided design, if the two temperatures are exactly equal there is no more propensity to turn one way than the other. The moment we look at it, it may be turning one way or the other, but in the long run, it gets nowhere. The fact that it gets nowhere is really the fundamental deep principle on which all of thermodynamics is based.
46–3Reversibility in mechanics
What deeper mechanical principle tells us that, in the long run, if the temperature is kept the same everywhere, our gadget will turn neither to the right nor to the left? We evidently have a fundamental proposition that there is no way to design a machine which, left to itself, will be more likely to be turning one way than the other after a long enough time. We must try to see how this follows from the laws of mechanics.
The laws of mechanics go something like this: the mass times the acceleration is the force, and the force on each particle is some complicated function of the positions of all the other particles. There are other situations in which forces depend on velocity, such as in magnetism, but let us not consider that now. We take a simpler case, such as gravity, where forces depend only on position. Now suppose that we have solved our set of equations and we have a certain motion $x(t)$ for each particle. In a complicated enough system, the solutions are very complicated, and what happens with time turns out to be very surprising. If we write down any arrangement we please for the particles, we will see this arrangement actually occur if we wait long enough! If we follow our solution for a long enough time, it tries everything that it can do, so to speak. This is not absolutely necessary in the simplest devices, but when systems get complicated enough, with enough atoms, it happens. Now there is something else the solution can do. If we solve the equations of motion, we may get certain functions such as $t + t^2 + t^3$. We claim that another solution would be $-t + t^2 - t^3$. In other words, if we substitute $-t$ everywhere for $t$ throughout the entire solution, we will once again get a solution of the same equation. This follows from the fact that if we substitute $-t$ for $t$ in the original differential equation, nothing is changed, since only second derivatives with respect to $t$ appear. This means that if we have a certain motion, then the exact opposite motion is also possible. In the complete confusion which comes if we wait long enough, it finds itself going one way sometimes, and it finds itself going the other way sometimes. There is nothing more beautiful about one of the motions than about the other. So it is impossible to design a machine which, in the long run, is more likely to be going one way than the other, if the machine is sufficiently complicated.
One might think up an example for which this is obviously untrue. If we take a wheel, for instance, and spin it in empty space, it will go the same way forever. So there are some conditions, like the conservation of angular momentum, which violate the above argument. This just requires that the argument be made with a little more care. Perhaps the walls take up the angular momentum, or something like that, so that we have no special conservation laws. Then, if the system is complicated enough, the argument is true. It is based on the fact that the laws of mechanics are reversible.
2022.12.21: 통찰
누군가 장기는 비기고 바둑은 먼저 두는 사람이 항상 이기게 되어 있다고 했단다.
12.23: 각운동량 보존 법칙에 대한 파인만 언급으로 부터... 물리 법칙와 수학 정리의 차이
물리는 에너지 보존 등 주로 geometrically local인 반면, 수학은 local은 물론 global한 걸 다룬다, 가우스-보넷 정리, 포앙카레-호프 정리 등.
그 필요성을 언급한 파인만, 두리뭉실 애매모호하게.
For historical interest, we would like to remark on a device invented by Maxwell, who first worked out the dynamical theory of gases. He supposed the following situation: We have two boxes of gas at the same temperature, with a little hole between them. At the hole sits a little demon (who may be a machine of course!). There is a door on the hole, which can be opened or closed by the demon. He watches the molecules coming from the left. Whenever he sees a fast molecule, he opens the door. When he sees a slow one, he leaves it closed. If we want him to be an extra special demon, he can have eyes at the back of his head, and do the opposite to the molecules from the other side. He lets the slow ones through to the left, and the fast through to the right. Pretty soon the left side will get cold and the right side hot. Then, are the ideas of thermodynamics violated because we could have such a demon?
It turns out, if we build a finite-sized demon, that the demon himself gets so warm that he cannot see very well after a while. The simplest possible demon, as an example, would be a trap door held over the hole by a spring. A fast molecule comes through, because it is able to lift the trap door. The slow molecule cannot get through, and bounces back. But this thing is nothing but our ratchet and pawl in another form, and ultimately the mechanism will heat up. If we assume that the specific heat of the demon is not infinite, it must heat up. It has but a finite number of internal gears and wheels, so it cannot get rid of the extra heat that it gets from observing the molecules. Soon it is shaking from Brownian motion so much that it cannot tell whether it is coming or going, much less whether the molecules are coming or going, so it does not work.
46–4Irreversibility
Are all the laws of physics reversible? Evidently not! Just try to unscramble an egg! Run a moving picture backwards, and it takes only a few minutes for everybody to start laughing. The most natural characteristic of all phenomena is their obvious irreversibility.
Where does irreversibility come from? It does not come from Newton’s laws. If we claim that the behavior of everything is ultimately to be understood in terms of the laws of physics, and if it also turns out that all the equations have the fantastic property that if we put $t = -t$ we have another solution, then every phenomenon is reversible. How then does it come about in nature on a large scale that things are not reversible? Obviously there must be some law, some obscure but fundamental equation, perhaps in electricity, maybe in neutrino physics, in which it does matter which way time goes.
Let us discuss that question now. We already know one of those laws, which says that the entropy is always increasing. If we have a hot thing and a cold thing, the heat goes from hot to cold. So the law of entropy is one such law. But we expect to understand the law of entropy from the point of view of mechanics. In fact, we have just been successful in obtaining all the consequences of the argument that heat cannot flow backwards by itself from just mechanical arguments, and we thereby obtained an understanding of the Second Law. Apparently we can get irreversibility from reversible equations. But was it only a mechanical argument that we used? Let us look into it more closely.
Since our question has to do with the entropy, our problem is to try to find a microscopic description of entropy. If we say we have a certain amount of energy in something, like a gas, then we can get a microscopic picture of it, and say that every atom has a certain energy. All these energies added together give us the total energy. Similarly, maybe every atom has a certain entropy. If we add everything up, we would have the total entropy. It does not work so well, but let us see what happens.
As an example, we calculate the entropy difference between a gas at a certain temperature at one volume, and a gas at the same temperature at another volume. We remember, from Chapter 44, that we had, for the change in entropy, \begin{equation*} \Delta S = \int\frac{dQ}{T}. \end{equation*} In the present case, the energy of the gas is the same before and after expansion, since the temperature does not change. So we have to add enough heat to equal the work done by the gas or, for each little change in volume, \begin{equation*} dQ = P\,dV. \end{equation*} Putting this in for $dQ$, we get \begin{align*} \Delta S &= \int_{V_1}^{V_2}P\,\frac{dV}{T} = \int_{V_1}^{V_2}\frac{NkT}{V}\,\frac{dV}{T}\\[.5ex] &= Nk\ln\frac{V_2}{V_1}, \end{align*} as we obtained in Chapter 44. For instance, if we expand the volume by a factor of $2$, the entropy change is $Nk\ln 2$.
Let us now consider another interesting example. Suppose we have a box with a barrier in the middle. On one side is neon (“black” molecules), and on the other, argon (“white” molecules). Now we take out the barrier, and let them mix. How much has the entropy changed? It is possible to imagine that instead of the barrier we have a piston, with holes in it that let the whites through but not the blacks, and another kind of piston which is the other way around. If we move one piston to each end, we see that, for each gas, the problem is like the one we just solved. So we get an entropy change of $Nk\ln 2$, which means that the entropy has increased by $k\ln 2$ per molecule. The $2$ has to do with the extra room that the molecule has, which is rather peculiar. It is not a property of the molecule itself, but of how much room the molecule has to run around in. This is a strange situation, where entropy increases but where everything has the same temperature and the same energy! The only thing that is changed is that the molecules are distributed differently.
2022.12.24: 온도, 에너지, 분자 갯수에 변화가 없으니 분자 자체의 문제가 당연히 아님
위에서 add enough heat to equal the work done by the gas라고 했듯이, 흑백 분자들은 장벽에 work on함으로 '움직임'(=活氣)을 저장하고 있었던 거.
46-2의 demon heat up 것과 마찬지로. 장벽이 제거된다는 건 그 움직임을 풀어주는 것이요 그로 인해 움직이는 기(活氣)가 늘어난 것.
12.25: 물리적 limit reversible, 움직임 손실이 없음을 가정함으로써, 온도 정의가 기의 움직임 척도로? 즉 $\lim_{마찰\to 0} T$ ⇨ the universal 온도 정의
12.27: 열(heat)는 질량을 말하지 않는다, thermal mass라는 것은 있는데.
열은 활기 덩어리고, 온도는 '기' 움직임 척도, 질량을 기의 structure로, 즉 질량은 기 바다에 잠겨있는 '기 구조물'로 정의.
We well know that if we just pull the barrier out, everything will get mixed up after a long time, due to the collisions, the jiggling, the banging, and so on. Every once in a while a white molecule goes toward a black, and a black one goes toward a white, and maybe they pass. Gradually the whites worm their way, by accident, across into the space of blacks, and the blacks worm their way, by accident, into the space of whites. If we wait long enough we get a mixture. Clearly, this is an irreversible process in the real world, and ought to involve an increase in the entropy.
Here we have a simple example of an irreversible process which is completely composed of reversible events. Every time there is a collision between any two molecules, they go off in certain directions. If we took a moving picture of a collision in reverse, there would be nothing wrong with the picture. In fact, one kind of collision is just as likely as another. So the mixing is completely reversible, and yet it is irreversible. Everyone knows that if we started with white and with black, separated, we would get a mixture within a few minutes. If we sat and looked at it for several more minutes, it would not separate again but would stay mixed. So we have an irreversibility which is based on reversible situations. But we also see the reason now. We started with an arrangement which is, in some sense, ordered. Due to the chaos of the collisions, it becomes disordered. It is the change from an ordered arrangement to a disordered arrangement which is the source of the irreversibility.
It is true that if we took a motion picture of this, and showed it backwards, we would see it gradually become ordered. Someone would say, “That is against the laws of physics!” So we would run the film over again, and we would look at every collision. Every one would be perfect, and every one would be obeying the laws of physics. The reason, of course, is that every molecule’s velocities are just right, so if the paths are all followed back, they get back to their original condition. But that is a very unlikely circumstance to have. If we start with the gas in no special arrangement, just whites and blacks, it will never get back.
46–5Order and entropy
So we now have to talk about what we mean by disorder and what we mean by order. It is not a question of pleasant order or unpleasant disorder. What is different in our mixed and unmixed cases is the following. Suppose we divide the space into little volume elements. If we have white and black molecules, how many ways could we distribute them among the volume elements so that white is on one side, and black on the other? On the other hand, how many ways could we distribute them with no restriction on which goes where? Clearly, there are many more ways to arrange them in the latter case. We measure “disorder” by the number of ways that the insides can be arranged, so that from the outside it looks the same. The logarithm of that number of ways is the entropy. The number of ways in the separated case is less, so the entropy is less, or the “disorder” is less.
So with the above technical definition of disorder we can understand the proposition. First, the entropy measures the disorder. Second, the universe always goes from “order” to “disorder,” so entropy always increases. Order is not order in the sense that we like the arrangement, but in the sense that the number of different ways we can hook it up, and still have it look the same from the outside, is relatively restricted. In the case where we reversed our motion picture of the gas mixing, there was not as much disorder as we thought. Every single atom had exactly the correct speed and direction to come out right! The entropy was not high after all, even though it appeared so.
What about the reversibility of the other physical laws? When we talked about the electric field which comes from an accelerating charge, it was said that we must take the retarded field. At a time $t$ and at a distance $r$ from the charge, we take the field due to the acceleration at a time $t - r/c$, not $t + r/c$. So it looks, at first, as if the law of electricity is not reversible. Very strangely, however, the laws we used come from a set of equations called Maxwell’s equations, which are, in fact, reversible. Furthermore, it is possible to argue that if we were to use only the advanced field, the field due to the state of affairs at $t + r/c$, and do it absolutely consistently in a completely enclosed space, everything happens exactly the same way as if we use retarded fields! This apparent irreversibility in electricity, at least in an enclosure, is thus not an irreversibility at all. We have some feeling for that already, because we know that when we have an oscillating charge which generates fields which are bounced from the walls of an enclosure we ultimately get to an equilibrium in which there is no one-sidedness. The retarded field approach is only a convenience in the method of solution.
So far as we know, all the fundamental laws of physics, like Newton’s equations, are reversible. Then where does irreversibility come from? It comes from order going to disorder, but we do not understand this until we know the origin of the order. Why is it that the situations we find ourselves in every day are always out of equilibrium? One possible explanation is the following. Look again at our box of mixed white and black molecules. Now it is possible, if we wait long enough, by sheer, grossly improbable, but possible, accident, that the distribution of molecules gets to be mostly white on one side and mostly black on the other. After that, as times goes on and accidents continue, they get more mixed up again.
Thus one possible explanation of the high degree of order in the present-day world is that it is just a question of luck. Perhaps our universe happened to have had a fluctuation of some kind in the past, in which things got somewhat separated, and now they are running back together again. This kind of theory is not unsymmetrical, because we can ask what the separated gas looks like either a little in the future or a little in the past. In either case, we see a grey smear at the interface, because the molecules are mixing again. No matter which way we run time, the gas mixes. So this theory would say the irreversibility is just one of the accidents of life.
We would like to argue that this is not the case. Suppose we do not look at the whole box at once, but only at a piece of the box. Then, at a certain moment, suppose we discover a certain amount of order. In this little piece, white and black are separate. What should we deduce about the condition in places where we have not yet looked? If we really believe that the order arose from complete disorder by a fluctuation, we must surely take the most likely fluctuation which could produce it, and the most likely condition is not that the rest of it has also become disentangled! Therefore, from the hypothesis that the world is a fluctuation, all of the predictions are that if we look at a part of the world we have never seen before, we will find it mixed up, and not like the piece we just looked at. If our order were due to a fluctuation, we would not expect order anywhere but where we have just noticed it.
Now we assume the separation is because the past of the universe was really ordered. It is not due to a fluctuation, but the whole thing used to be white and black. This theory now predicts that there will be order in other places—the order is not due to a fluctuation, but due to a much higher ordering at the beginning of time. Then we would expect to find order in places where we have not yet looked.
2022.12.25: 파인만 talking about some sort of a global thing such as 포앙카레-호프 정리, zero-sum
The astronomers, for example, have only looked at some of the stars. Every day they turn their telescopes to other stars, and the new stars are doing the same thing as the other stars. We therefore conclude that the universe is not a fluctuation, and that the order is a memory of conditions when things started. This is not to say that we understand the logic of it. For some reason, the universe at one time had a very low entropy for its energy content, and since then the entropy has increased. So that is the way toward the future. That is the origin of all irreversibility, that is what makes the processes of growth and decay, that makes us remember the past and not the future, remember the things which are closer to that moment in the history of the universe when the order was higher than now, and why we are not able to remember things where the disorder is higher than now, which we call the future. So, as we commented in an earlier chapter, the entire universe is in a glass of wine, if we look at it closely enough. In this case the glass of wine is complex, because there is water and glass and light and everything else.
2022.12.26: 엔트로피가 항상 증가한다는 건 열 에너지 측면에서 설명한 것, 인간 경험적으로 열은 높은 곳에서 낮은 곳으로 흐른다는. 그런데 말야, 높은 온도의 기체가 낮은 기체를 만나면 서로 섞이면서 평균을 찾는 거니, 낮은 기체가 높은 기체에 영향을 주는 건 확실하잖아, 그리고 움직임의 흐름으로 보면 낮은 게 높은 곳으로 이동도 하고.
Another delight of our subject of physics is that even simple and idealized things, like the ratchet and pawl, work only because they are part of the universe. The ratchet and pawl works in only one direction because it has some ultimate contact with the rest of the universe. If the ratchet and pawl were in a box and isolated for some sufficient time, the wheel would be no more likely to go one way than the other. But because we pull up the shades and let the light out, because we cool off on the earth and get heat from the sun, the ratchets and pawls that we make can turn one way. This one-wayness is interrelated with the fact that the ratchet is part of the universe. It is part of the universe not only in the sense that it obeys the physical laws of the universe, but its one-way behavior is tied to the one-way behavior of the entire universe. It cannot be completely understood until the mystery of the beginnings of the history of the universe are reduced still further from speculation to scientific understanding.
- See Parrondo and Español, Am. J. Phys. 64, 1125 (1996) for a critical analysis of this chapter. ↩