4 Electrostatics
Electrostatics
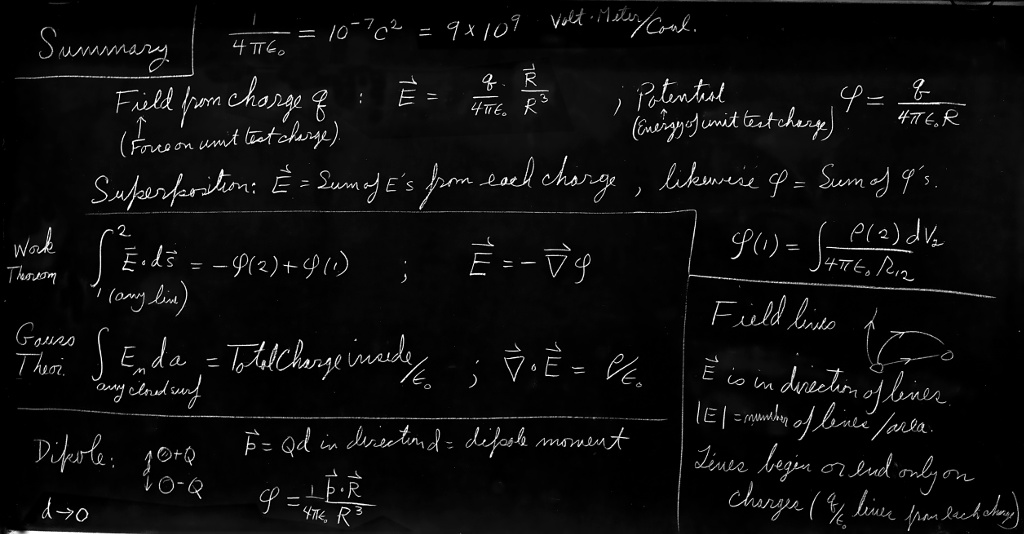
| Review: | Chapters 13, and 14 Vol. I, Work and Potential Energy |
4–1Statics
We begin now our detailed study of the theory of
electromagnetism. All of electromagnetism is contained in the Maxwell
equations.
Maxwell’s equations:
\begin{align}
\label{Eq:II:4:1}
\FLPdiv{\FLPE}&=\frac{\rho}{\epsO},\\[1ex]
\label{Eq:II:4:2}
\FLPcurl{\FLPE}&=-\ddp{\FLPB}{t},\\[1ex]
\label{Eq:II:4:3}
c^2\,\FLPcurl{\FLPB}&=\ddp{\FLPE}{t}+\frac{\FLPj}{\epsO},\\[1ex]
\label{Eq:II:4:4}
\FLPdiv{\FLPB}&=0.
\end{align}
The situations that are described by these equations can be very
complicated. We will consider first relatively simple situations, and
learn how to handle them before we take up more complicated ones. The
easiest circumstance to treat is one in which nothing depends on the
time—called the static case. All charges are permanently
fixed in space, or if they do move, they move as a steady flow in a
circuit (so $\rho$ and $\FLPj$ are constant in time). In these
circumstances, all of the terms in the Maxwell equations which are time derivatives
of the field are zero. In this case, the Maxwell
equations
become:
Electrostatics:
\begin{align}
\label{Eq:II:4:5}
\FLPdiv{\FLPE}&=\frac{\rho}{\epsO},\\[1ex]
\label{Eq:II:4:6}
\FLPcurl{\FLPE}&=\FLPzero.
\end{align}
Magnetostatics:
\begin{align}
\label{Eq:II:4:7}
\FLPcurl{\FLPB}&=\frac{\FLPj}{\epsO c^2},\\[1ex]
\label{Eq:II:4:8}
\FLPdiv{\FLPB}&=0.
\end{align}
You will notice an interesting thing about this set of four equations. It can be separated into two pairs. The electric field $\FLPE$ appears only in the first two, and the magnetic field $\FLPB$ appears only in the second two. The two fields are not interconnected. This means that electricity and magnetism are distinct phenomena so long as charges and currents are static. The interdependence of $\FLPE$ and $\FLPB$ does not appear until there are changes in charges or currents, as when a condensor is charged, or a magnet moved. Only when there are sufficiently rapid changes, so that the time derivatives in Maxwell’s equations become significant, will $\FLPE$ and $\FLPB$ depend on each other.
Now if you look at the equations of statics you will see that the study of the two subjects we call electrostatics and magnetostatics is ideal from the point of view of learning about the mathematical properties of vector fields. Electrostatics is a neat example of a vector field with zero curl and a given divergence. Magnetostatics is a neat example of a field with zero divergence and a given curl. The more conventional—and you may be thinking, more satisfactory—way of presenting the theory of electromagnetism is to start first with electrostatics and thus to learn about the divergence. Magnetostatics and the curl are taken up later. Finally, electricity and magnetism are put together. We have chosen to start with the complete theory of vector calculus. Now we shall apply it to the special case of electrostatics, the field of $\FLPE$ given by the first pair of equations.
We will begin with the simplest situations—ones in which the positions of all charges are specified. If we had only to study electrostatics at this level (as we shall do in the next two chapters), life would be very simple—in fact, almost trivial. Everything can be obtained from Coulomb’s law and some integration, as you will see. In many real electrostatic problems, however, we do not know, initially, where the charges are. We know only that they have distributed themselves in ways that depend on the properties of matter. The positions that the charges take up depend on the $\FLPE$ field, which in turn depends on the positions of the charges. Then things can get quite complicated. If, for instance, a charged body is brought near a conductor or insulator, the electrons and protons in the conductor or insulator will move around. The charge density $\rho$ in Eq. (4.5) may have one part that we know about, from the charge that we brought up; but there will be other parts from charges that have moved around in the conductor. And all of the charges must be taken into account. One can get into some rather subtle and interesting problems. So although this chapter is to be on electrostatics, it will not cover the more beautiful and subtle parts of the subject. It will treat only the situation where we can assume that the positions of all the charges are known. Naturally, you should be able to do that case before you try to handle the other ones.
4–2Coulomb’s law; superposition
It would be logical to use Eqs. (4.5) and (4.6)
as our starting points. It will be easier, however, if we start somewhere else
and come back to these equations. The results will be equivalent. We will start
with a law that we have talked about before, called Coulomb’s law, which says
that between two charges at rest there is a force directly proportional to the
product of the charges and inversely proportional to the square of the distance
between. The force is along the straight line from one charge to the other.
Coulomb’s law:
\begin{equation}
\label{Eq:II:4:9}
\FLPF_1=\frac{1}{4\pi\epsO}\,\frac{q_1q_2}{r_{12}^2}\,\FLPe_{12}=-\FLPF_2.
\end{equation}
$\FLPF_1$ is the force on charge $q_1$, $\FLPe_{12}$ is the
unit vector in the direction to $q_1$ from $q_2$,
and $r_{12}$ is the distance between $q_1$ and $q_2$. The
force $\FLPF_2$ on $q_2$ is equal and opposite to $\FLPF_1$.
The constant of proportionality, for historical reasons, is written as $1/4\pi\epsO$. In the system of units which we use—the mks system—it is defined as exactly $10^{-7}$ times the speed of light squared. Now since the speed of light is approximately $3\times10^8$ meters per second, the constant is approximately $9\times10^9$, and the unit turns out to be newton$\cdot$meter$^2$ per coulomb$^2$ or volt$\cdot$meter per coulomb. \begin{align} \frac{1}{4\pi\epsO}&=10^{-7}c^2\;\quad\,\text{(by definition)}\notag\\[-1pt] \label{Eq:II:4:10} &=9.0\times10^9\;\text{(by experiment).}\\[2pt] \text{Unit:}&\quad\text{newton$\cdot$meter$^2$$/$coulomb$^2$,}\notag\\[2pt] \text{or}&\quad\text{volt$\cdot$meter$/$coulomb.}\notag \end{align}
When there are more than two charges present—the only really interesting times—we must supplement Coulomb’s law with one other fact of nature: the force on any charge is the vector sum of the Coulomb forces from each of the other charges. This fact is called “the principle of superposition.” That’s all there is to electrostatics. If we combine the Coulomb law and the principle of superposition, there is nothing else. Equations (4.5) and (4.6)—the electrostatic equations—say no more and no less.
When applying Coulomb’s law, it is convenient to introduce the idea of an electric field. We say that the field $\FLPE(1)$ is the force per unit charge on $q_1$ (due to all other charges). Dividing Eq. (4.9) by $q_1$, we have, for one other charge besides $q_1$, \begin{equation} \label{Eq:II:4:11} \FLPE(1)=\frac{1}{4\pi\epsO}\,\frac{q_2}{r_{12}^2}\,\FLPe_{12}. \end{equation} Also, we consider that $\FLPE(1)$ describes something about the point $(1)$ even if $q_1$ were not there—assuming that all other charges keep their same positions. We say: $\FLPE(1)$ is the electric field at the point $(1)$.
The electric field $\FLPE$ is a vector, so by Eq. (4.11) we really mean three equations—one for each component. Writing out explicitly the $x$-component, Eq. (4.11) means \begin{equation} \label{Eq:II:4:12} E_x(x_1,y_1,z_1)=\frac{q_2}{4\pi\epsO}\, \frac{x_1-x_2}{[(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2]^{3/2}}, \end{equation} and similarly for the other components.
If there are many charges present, the field $\FLPE$ at any point $(1)$ is a sum of the contributions from each of the other charges. Each term of the sum will look like (4.11) or (4.12). Letting $q_j$ be the magnitude of the $j$th charge, and $\FLPr_{1j}$ the displacement from $q_j$ to the point $(1)$, we write \begin{equation} \label{Eq:II:4:13} \FLPE(1)=\sum_j\frac{1}{4\pi\epsO}\,\frac{q_j}{r_{1j}^2}\,\FLPe_{1j}. \end{equation} Which means, of course, \begin{equation} \label{Eq:II:4:14} E_x(x_1,y_1,z_1)=\sum_j\frac{1}{4\pi\epsO}\, \frac{q_j(x_1-x_j)}{[(x_1-x_j)^2+(y_1-y_j)^2+(z_1-z_j)^2]^{3/2}}, \end{equation} and so on.
Often it is convenient to ignore the fact that charges come in packages like electrons and protons, and think of them as being spread out in a continuous smear—or in a “distribution,” as it is called. This is O.K. so long as we are not interested in what is happening on too small a scale. We describe a charge distribution by the “charge density,” $\rho(x,y,z)$. If the amount of charge in a small volume $\Delta V_2$ located at the point $(2)$ is $\Delta q_2$, then $\rho$ is defined by \begin{equation} \label{Eq:II:4:15} \Delta q_2=\rho(2)\Delta V_2. \end{equation}
To use Coulomb’s law with such a description, we replace the sums of Eqs. (4.13) or (4.14) by integrals over all volumes containing charges. Then we have \begin{equation} \label{Eq:II:4:16} \FLPE(1)=\frac{1}{4\pi\epsO} \underset{\substack{\text{all}\\\text{space}}}{\int} \frac{\rho(2)\FLPe_{12}\,dV_2}{r_{12}^2}. \end{equation} Some people prefer to write \begin{equation*} \FLPe_{12}=\frac{\FLPr_{12}}{r_{12}},\notag \end{equation*} where $\FLPr_{12}$ is the vector displacement to $(1)$ from $(2)$, as shown in Fig. 4-1. The integral for $\FLPE$ is then written as \begin{equation} \label{Eq:II:4:17} \FLPE(1)=\frac{1}{4\pi\epsO} \underset{\substack{\text{all}\\\text{space}}}{\int} \frac{\rho(2)\FLPr_{12}\,dV_2}{r_{12}^3}. \end{equation} When we want to calculate something with these integrals, we usually have to write them out in explicit detail. For the $x$-component of either Eq. (4.16) or (4.17), we would have \begin{equation} \label{Eq:II:4:18} E_x(x_1,y_1,z_1)= \underset{\substack{\text{all}\\\text{space}}}{\int} \frac{(x_1-x_2)\rho(x_2,y_2,z_2)\,dx_2\,dy_2\,dz_2} {4\pi\epsO [(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2]^{3/2}}. \end{equation}
We are not going to use this formula much. We write it here only to emphasize the fact that we have completely solved all the electrostatic problems in which we know the locations of all of the charges. Given the charges, what are the fields? Answer: Do this integral. So there is nothing to the subject; it is just a case of doing complicated integrals over three dimensions—strictly a job for a computing machine!
With our integrals we can find the fields produced by a sheet of charge, from a line of charge, from a spherical shell of charge, or from any specified distribution. It is important to realize, as we go on to draw field lines, to talk about potentials, or to calculate divergences, that we already have the answer here. It is merely a matter of it being sometimes easier to do an integral by some clever guesswork than by actually carrying it out. The guesswork requires learning all kinds of strange things. In practice, it might be easier to forget trying to be clever and always to do the integral directly instead of being so smart. We are, however, going to try to be smart about it. We shall go on to discuss some other features of the electric field.
4–3Electric potential
First we take up the idea of electric potential, which is related to the work done in carrying a charge from one point to another. There is some distribution of charge, which produces an electric field. We ask about how much work it would take to carry a small charge from one place to another. The work done against the electrical forces in carrying a charge along some path is the negative of the component of the electrical force in the direction of the motion, integrated along the path. If we carry a charge from point $a$ to point $b$, \begin{equation*} W=-\int_a^b\FLPF\cdot d\FLPs, \end{equation*} where $\FLPF$ is the electrical force on the charge at each point, and $d\FLPs$ is the differential vector displacement along the path. (See Fig. 4-2.)
It is more interesting for our purposes to consider the work that would be done in carrying one unit of charge. Then the force on the charge is numerically the same as the electric field. Calling the work done against electrical forces in this case $W(\text{unit})$, we write \begin{equation} \label{Eq:II:4:19} W(\text{unit})=-\int_a^b\FLPE\cdot d\FLPs. \end{equation} Now, in general, what we get with this kind of an integral depends on the path we take. But if the integral of (4.19) depended on the path from $a$ to $b$, we could get work out of the field by carrying the charge to $b$ along one path and then back to $a$ on the other. We would go to $b$ along the path for which $W$ is smaller and back along the other, getting out more work than we put in.
There is nothing impossible, in principle, about getting energy out of a field. We shall, in fact, encounter fields where it is possible. It could be that as you move a charge you produce forces on the other part of the “machinery.” If the “machinery” moved against the force it would lose energy, thereby keeping the total energy in the world constant. For electrostatics, however, there is no such “machinery.” We know what the forces back on the sources of the field are. They are the Coulomb forces on the charges responsible for the field. If the other charges are fixed in position—as we assume in electrostatics only—these back forces can do no work on them. There is no way to get energy from them—provided, of course, that the principle of energy conservation works for electrostatic situations. We believe that it will work, but let’s just show that it must follow from Coulomb’s law of force.
We consider first what happens in the field due to a single charge $q$. Let point $a$ be at the distance $r_a$ from $q$, and point $b$ at $r_b$. Now we carry a different charge, which we will call the “test” charge, and whose magnitude we choose to be one unit, from $a$ to $b$. Let’s start with the easiest possible path to calculate. We carry our test charge first along the arc of a circle, then along a radius, as shown in part (a) of Fig. 4-3. Now on that particular path it is child’s play to find the work done (otherwise we wouldn’t have picked it). First, there is no work done at all on the path from $a$ to $a'$. The field is radial (from Coulomb’s law), so it is at right angles to the direction of motion. Next, on the path from $a'$ to $b$, the field is in the direction of motion and varies as $1/r^2$. Thus the work done on the test charge in carrying it from $a$ to $b$ would be \begin{equation} \label{Eq:II:4:20} -\int_a^b\FLPE\cdot d\FLPs=-\frac{q}{4\pi\epsO}\int_{a'}^b \frac{dr}{r^2}=-\frac{q}{4\pi\epsO} \biggl(\frac{1}{r_a}-\frac{1}{r_b}\biggr). \end{equation}
Now let’s take another easy path. For instance, the one shown in part (b) of Fig. 4-3. It goes for awhile along an arc of a circle, then radially for awhile, then along an arc again, then radially, and so on. Every time we go along the circular parts, we do no work. Every time we go along the radial parts, we must just integrate $1/r^2$. Along the first radial stretch, we integrate from $r_a$ to $r_{a'}$, then along the next radial stretch from $r_{a'}$ to $r_{a''}$, and so on. The sum of all these integrals is the same as a single integral directly from $r_a$ to $r_b$. We get the same answer for this path that we did for the first path we tried. It is clear that we would get the same answer for any path which is made up of an arbitrary number of the same kinds of pieces.
What about smooth paths? Would we get the same answer? We discussed this point previously in Chapter 13 of Vol. I. Applying the same arguments used there, we can conclude that work done in carrying a unit charge from $a$ to $b$ is independent of the path. \begin{equation*} \left.\begin{gathered} W(\text{unit})\\[1ex] a\to b \end{gathered} \right\} =-\underset{\substack{\text{any}\\\text{path}}}{\int_a^b}\FLPE\cdot d\FLPs. \end{equation*}
Since the work done depends only on the endpoints, it can be represented as the difference between two numbers. We can see this in the following way. Let’s choose a reference point $P_0$ and agree to evaluate our integral by using a path that always goes by way of point $P_0$. Let $\phi(a)$ stand for the work done against the field in going from $P_0$ to point $a$, and let $\phi(b)$ be the work done in going from $P_0$ to point $b$ (Fig. 4-4). The work in going to $P_0$ from $a$ (on the way to $b$) is the negative of $\phi(a)$, so we have that \begin{equation} \label{Eq:II:4:21} -\int_a^b\FLPE\cdot d\FLPs=\phi(b)-\phi(a). \end{equation}
Since only the difference in the function $\phi$ at two points is ever
involved, we do not really have to specify the location of $P_0$. Once
we have chosen some reference point, however, a number $\phi$ is
determined for any point in space; $\phi$ is then a
scalar field. It is a function of $x$, $y$, $z$. We call this scalar
function the electrostatic potential at any point.
Electrostatic potential:
\begin{equation}
\label{Eq:II:4:22}
\phi(P)=-\int_{P_0}^P\FLPE\cdot d\FLPs.
\end{equation}
For convenience, we will often take the reference point at infinity. Then, for a single charge at the origin, the potential $\phi$ is given for any point $(x,y,z)$—using Eq. (4.20): \begin{equation} \label{Eq:II:4:23} \phi(x,y,z)=\frac{q}{4\pi\epsO}\,\frac{1}{r}. \end{equation}
The electric field from several charges can be written as the sum of the electric field from the first, from the second, from the third, etc. When we integrate the sum to find the potential we get a sum of integrals. Each of the integrals is the negative of the potential from one of the charges. We conclude that the potential $\phi$ from a lot of charges is the sum of the potentials from all the individual charges. There is a superposition principle also for potentials. Using the same kind of arguments by which we found the electric field from a group of charges and for a distribution of charges, we can get the complete formulas for the potential $\phi$ at a point we call $(1)$: \begin{align} \label{Eq:II:4:24} \phi(1)&=\sum_{j}\frac{1}{4\pi\epsO}\,\frac{q_j}{r_{1j}},\\[1ex] \label{Eq:II:4:25} \phi(1)&=\frac{1}{4\pi\epsO} \underset{\substack{\text{all}\\\text{space}}}{\int} \frac{\rho(2)\,dV_2}{r_{12}}. \end{align}
Remember that the potential $\phi$ has a physical significance: it is the potential energy which a unit charge would have if brought to the specified point in space from some reference point.
4–4$\boldsymbol{E=-\nabla\phi}$
Who cares about $\phi$? Forces on charges are given by $\FLPE$, the electric field. The point is that $\FLPE$ can be obtained easily from $\phi$—it is as easy, in fact, as taking a derivative. Consider two points, one at $x$ and one at $(x+\Delta x)$, but both at the same $y$ and $z$, and ask how much work is done in carrying a unit charge from one point to the other. The path is along the horizontal line from $x$ to $x+\Delta x$. The work done is the difference in the potential at the two points: \begin{equation*} \Delta W=\phi(x+\Delta x,y,z)-\phi(x,y,z)=\ddp{\phi}{x}\,\Delta x. \end{equation*} But the work done against the field for the same path is \begin{equation*} \Delta W=-\int\FLPE\cdot d\FLPs=-E_x\,\Delta x. \end{equation*} We see that \begin{equation} \label{Eq:II:4:26} E_x=-\ddp{\phi}{x}. \end{equation} Similarly, $E_y=-\ddpl{\phi}{y}$, $E_z=-\ddpl{\phi}{z}$, or, summarizing with the notation of vector analysis, \begin{equation} \label{Eq:II:4:27} \FLPE=-\FLPgrad{\phi}. \end{equation} This equation is the differential form of Eq. (4.22). Any problem with specified charges can be solved by computing the potential from (4.24) or (4.25) and using (4.27) to get the field. Equation (4.27) also agrees with what we found from vector calculus: that for any scalar field $\phi$ \begin{equation} \label{Eq:II:4:28} \int_a^b\FLPgrad{\phi}\cdot d\FLPs=\phi(b)-\phi(a). \end{equation}
According to Eq. (4.25) the scalar potential $\phi$ is given by a three-dimensional integral similar to the one we had for $\FLPE$. Is there any advantage to computing $\phi$ rather than $\FLPE$? Yes. There is only one integral for $\phi$, while there are three integrals for $\FLPE$—because it is a vector. Furthermore, $1/r$ is usually a little easier to integrate than $x/r^3$. It turns out in many practical cases that it is easier to calculate $\phi$ and then take the gradient to find the electric field, than it is to evaluate the three integrals for $\FLPE$. It is merely a practical matter.
There is also a deeper physical significance to the potential $\phi$. We have shown that $\FLPE$ of Coulomb’s law is obtained from $\FLPE=-\grad\phi$, when $\phi$ is given by (4.22). But if $\FLPE$ is equal to the gradient of a scalar field, then we know from the vector calculus that the curl of $\FLPE$ must vanish: \begin{equation} \label{Eq:II:4:29} \FLPcurl{\FLPE}=\FLPzero. \end{equation} But that is just our second fundamental equation of electrostatics, Eq. (4.6). We have shown that Coulomb’s law gives an $\FLPE$ field that satisfies that condition. So far, everything is all right.
We had really proved that $\FLPcurl{\FLPE}$ was zero before we defined the potential. We had shown that the work done around a closed path is zero. That is, that \begin{equation*} \oint\FLPE\cdot d\FLPs = 0 \end{equation*} for any path. We saw in Chapter 3 that for any such field $\FLPcurl{\FLPE}$ must be zero everywhere. The electric field in electrostatics is an example of a curl-free field.
You can practice your vector calculus by proving that $\FLPcurl{\FLPE}$ is zero in a different way—by computing the components of $\FLPcurl{\FLPE}$ for the field of a point charge, as given by Eq. (4.11). If you get zero, the superposition principle says you would get zero for the field of any charge distribution.
We should point out an important fact. For any radial force the work done is independent of the path, and there exists a potential. If you think about it, the entire argument we made above to show that the work integral was independent of the path depended only on the fact that the force from a single charge was radial and spherically symmetric. It did not depend on the fact that the dependence on distance was as $1/r^2$—there could have been any $r$ dependence. The existence of a potential, and the fact that the curl of $\FLPE$ is zero, comes really only from the symmetry and direction of the electrostatic forces. Because of this, Eq. (4.28)—or (4.29)—can contain only part of the laws of electricity.
4–5The flux of $\FLPE$
We will now derive a field equation that depends specifically and directly on the fact that the force law is inverse square. That the field varies inversely as the square of the distance seems, for some people, to be “only natural,” because “that’s the way things spread out.” Take a light source with light streaming out: the amount of light that passes through a surface cut out by a cone with its apex at the source is the same no matter at what radius the surface is placed. It must be so if there is to be conservation of light energy. The amount of light per unit area—the intensity—must vary inversely as the area cut by the cone, i.e., inversely as the square of the distance from the source. Certainly the electric field should vary inversely as the square of the distance for the same reason! But there is no such thing as the “same reason” here. Nobody can say that the electric field measures the flow of something like light which must be conserved. If we had a “model” of the electric field in which the electric field vector represented the direction and speed—say the current—of some kind of little “bullets” which were flying out, and if our model required that these bullets were conserved, that none could ever disappear once it was shot out of a charge, then we might say that we can “see” that the inverse square law is necessary. On the other hand, there would necessarily be some mathematical way to express this physical idea. If the electric field were like conserved bullets going out, then it would vary inversely as the square of the distance and we would be able to describe that behavior by an equation—which is purely mathematical. Now there is no harm in thinking this way, so long as we do not say that the electric field is made out of bullets, but realize that we are using a model to help us find the right mathematics.
Suppose, indeed, that we imagine for a moment that the electric field did represent the flow of something that was conserved—everywhere, that is, except at charges. (It has to start somewhere!) We imagine that whatever it is flows out of a charge into the space around. If $\FLPE$ were the vector of such a flow (as $\FLPh$ is for heat flow), it would have a $1/r^2$ dependence near a point source. Now we wish to use this model to find out how to state the inverse square law in a deeper or more abstract way, rather than simply saying “inverse square.” (You may wonder why we should want to avoid the direct statement of such a simple law, and want instead to imply the same thing sneakily in a different way. Patience! It will turn out to be useful.)
We ask: What is the “flow” of $\FLPE$ out of an arbitrary closed surface in the neighborhood of a point charge? First let’s take an easy surface—the one shown in Fig. 4-5. If the $\FLPE$ field is like a flow, the net flow out of this box should be zero. That is what we get if by the “flow” from this surface we mean the surface integral of the normal component of $\FLPE$—that is, the flux of $\FLPE$. On the radial faces, the normal component is zero. On the spherical faces, the normal component $E_n$ is just the magnitude of $\FLPE$—minus for the smaller face and plus for the larger face. The magnitude of $\FLPE$ decreases as $1/r^2$, but the surface area is proportional to $r^2$, so the product is independent of $r$. The flux of $\FLPE$ into face $a$ is just cancelled by the flux out of face $b$. The total flow out of $S$ is zero, which is to say that for this surface \begin{equation} \label{Eq:II:4:30} \int_S E_n\,da=0. \end{equation}
Next we show that the two end surfaces may be tilted with respect to the radial line without changing the integral (4.30). Although it is true in general, for our purposes it is only necessary to show that this is true when the end surfaces are small, so that they subtend a small angle from the source—in fact, an infinitesimal angle. In Fig. 4-6 we show a surface $S$ whose “sides” are radial, but whose “ends” are tilted. The end surfaces are not small in the figure, but you are to imagine the situation for very small end surfaces. Then the field $\FLPE$ will be sufficiently uniform over the surface that we can use just its value at the center. When we tilt the surface by an angle $\theta$, the area is increased by the factor $1/\cos\theta$. But $E_n$, the component of $\FLPE$ normal to the surface, is decreased by the factor $\cos\theta$. The product $E_n\,\Delta a$ is unchanged. The flux out of the whole surface $S$ is still zero.
Now it is easy to see that the flux out of a volume enclosed by any surface $S$ must be zero. Any volume can be thought of as made up of pieces, like that in Fig. 4-6. The surface will be subdivided completely into pairs of end surfaces, and since the fluxes in and out of these end surfaces cancel by pairs, the total flux out of the surface will be zero. The idea is illustrated in Fig. 4-7. We have the completely general result that the total flux of $\FLPE$ out of any surface $S$ in the field of a point charge is zero.
But notice! Our proof works only if the surface $S$ does not surround the charge. What would happen if the point charge were inside the surface? We could still divide our surface into pairs of areas that are matched by radial lines through the charge, as shown in Fig. 4-8. The fluxes through the two surfaces are still equal—by the same arguments as before—only now they have the same sign. The flux out of a surface that surrounds a charge is not zero. Then what is it? We can find out by a little trick. Suppose we “remove” the charge from the “inside” by surrounding the charge by a little surface $S'$ totally inside the original surface $S$, as shown in Fig. 4-9. Now the volume enclosed between the two surfaces $S$ and $S'$ has no charge in it. The total flux out of this volume (including that through $S'$) is zero, by the arguments we have given above. The arguments tell us, in fact, that the flux into the volume through $S'$ is the same as the flux outward through $S$.
We can choose any shape we wish for $S'$, so let’s make it a sphere centered on the charge, as in Fig. 4-10. Then we can easily calculate the flux through it. If the radius of the little sphere is $r$, the value of $\FLPE$ everywhere on its surface is \begin{equation*} \frac{1}{4\pi\epsO}\,\frac{q}{r^2}, \end{equation*} and is directed always normal to the surface. We find the total flux through $S'$ if we multiply this normal component of $\FLPE$ by the surface area: \begin{equation} \label{Eq:II:4:31} \text{Flux through the surface $S'$}= \biggl(\frac{1}{4\pi\epsO}\,\frac{q}{r^2}\biggr) (4\pi r^2)=\frac{q}{\epsO}, \end{equation} a number independent of the radius of the sphere! We know then that the flux outward through $S$ is also $q/\epsO$—a value independent of the shape of $S$ so long as the charge $q$ is inside.
We can write our conclusions as follows: \begin{equation} \label{Eq:II:4:32} \underset{\substack{\text{any closed}\\\text{surface $S$}}}{\int}\kern{-1em} E_n\,da = \begin{cases} 0;&\text{$q$ outside $S$}\\[1ex] {\dfrac{q}{\epsO}};&\text{$q$ inside $S$} \end{cases} \end{equation}
Let’s return to our “bullet” analogy and see if it makes sense. Our theorem says that the net flow of bullets through a surface is zero if the surface does not enclose the gun that shoots the bullets. If the gun is enclosed in a surface, whatever size and shape it is, the number of bullets passing through is the same—it is given by the rate at which bullets are generated at the gun. It all seems quite reasonable for conserved bullets. But does the model tell us anything more than we get simply by writing Eq. (4.32)? No one has succeeded in making these “bullets” do anything else but produce this one law. After that, they produce nothing but errors. That is why today we prefer to represent the electromagnetic field purely abstractly.
4–6Gauss’ law; the divergence of $\FLPE$
Our nice result, Eq. (4.32), was proved for a single point charge. Now suppose that there are two charges, a charge $q_1$ at one point and a charge $q_2$ at another. The problem looks more difficult. The electric field whose normal component we integrate for the flux is the field due to both charges. That is, if $\FLPE_1$ represents the electric field that would have been produced by $q_1$ alone, and $\FLPE_2$ represents the electric field produced by $q_2$ alone, the total electric field is $\FLPE=\FLPE_1+\FLPE_2$. The flux through any closed surface $S$ is \begin{equation} \label{Eq:II:4:33} \int_S(E_{1n}\!+\!E_{2n})\,da=\!\!\int_S E_{1n}\,da+\!\!\int_S E_{2n}\,da. \end{equation} The flux with both charges present is the flux due to a single charge plus the flux due to the other charge. If both charges are outside $S$, the flux through $S$ is zero. If $q_1$ is inside $S$ but $q_2$ is outside, then the first integral gives $q_1/\epsO$ and the second integral gives zero. If the surface encloses both charges, each will give its contribution and we have that the flux is $(q_1+q_2)/\epsO$. The general rule is clearly that the total flux out of a closed surface is equal to the total charge inside, divided by $\epsO$.
Our result is an important general law of the electrostatic field,
called Gauss’ law.
Gauss’ law:
\begin{equation}
\label{Eq:II:4:34}
\underset{\substack{\text{any closed}\\\text{surface $S$}}}{\int}\kern{-.5ex}
E_n\,da=\frac{\text{sum of charges inside}}{\epsO},
\end{equation}
or
\begin{equation}
\label{Eq:II:4:35}
\underset{\substack{\text{any closed}\\\text{surface $S$}}}{\int}
\FLPE\cdot\FLPn\,da=\frac{Q_{\text{int}}}{\epsO},
\end{equation}
where
\begin{equation}
\label{Eq:II:4:36}
Q_{\text{int}}=\underset{\text{inside $S$}}{\sum}q_i.
\end{equation}
If we describe the location of charges in terms of a charge
density $\rho$, we can consider that each infinitesimal volume $dV$ contains a
“point” charge $\rho\,dV$. The sum over all charges is then the
integral
\begin{equation}
\label{Eq:II:4:37}
Q_{\text{int}}=\kern{-1ex}
\underset{\substack{\text{volume}\\\text{inside $S$}}}{\int}
\rho\,dV.
\end{equation}
From our derivation you see that Gauss’ law follows from the fact that the exponent in Coulomb’s law is exactly two. A $1/r^3$ field, or any $1/r^n$ field with $n\neq2$, would not give Gauss’ law. So Gauss’ law is just an expression, in a different form, of the Coulomb law of forces between two charges. In fact, working back from Gauss’ law, you can derive Coulomb’s law. The two are quite equivalent so long as we keep in mind the rule that the forces between charges are radial.
We would now like to write Gauss’ law in terms of derivatives. To do this, we apply Gauss’ law to an infinitesimal cubical surface. We showed in Chapter 3 that the flux of $\FLPE$ out of such a cube is $\FLPdiv{\FLPE}$ times the volume $dV$ of the cube. The charge inside of $dV$, by the definition of $\rho$, is equal to $\rho\,dV$, so Gauss’ law gives \begin{equation*} \FLPdiv{\FLPE}\,dV=\frac{\rho\,dV}{\epsO}, \end{equation*} or \begin{equation} \label{Eq:II:4:38} \FLPdiv{\FLPE}=\frac{\rho}{\epsO}. \end{equation} The differential form of Gauss’ law is the first of our fundamental field equations of electrostatics, Eq. (4.5). We have now shown that the two equations of electrostatics, Eqs. (4.5) and (4.6), are equivalent to Coulomb’s law of force. We will now consider one example of the use of Gauss’ law. (We will come later to many more examples.)
4–7Field of a sphere of charge
One of the difficult problems we had when we studied the theory of gravitational attractions was to prove that the force produced by a solid sphere of matter was the same at the surface of the sphere as it would be if all the matter were concentrated at the center. For many years Newton didn’t make public his theory of gravitation, because he couldn’t be sure this theorem was true. We proved the theorem in Chapter 13 of Vol. I by doing the integral for the potential and then finding the gravitational force by using the gradient. Now we can prove the theorem in a most simple fashion. Only this time we will prove the corresponding theorem for a uniform sphere of electrical charge. (Since the laws of electrostatics are the same as those of gravitation, the same proof could be done for the gravitational field.)
We ask: What is the electric field $\FLPE$ at a point $P$ anywhere outside the surface of a sphere filled with a uniform distribution of charge? Since there is no “special” direction, we can assume that $\FLPE$ is everywhere directed away from the center of the sphere. We consider an imaginary surface that is spherical and concentric with the sphere of charge, and that passes through the point $P$ (Fig. 4-11). For this surface, the flux outward is \begin{equation*} \int E_n\,da=E\cdot4\pi R^2. \end{equation*} Gauss’ law tells us that this flux is equal to the total charge $Q$ of the sphere (over $\epsO$): \begin{equation*} E\cdot4\pi R^2=\frac{Q}{\epsO}, \end{equation*} or \begin{equation} \label{Eq:II:4:39} E=\frac{1}{4\pi\epsO}\,\frac{Q}{R^2}, \end{equation} which is the same formula we would have for a point charge $Q$. We have proved Newton’s problem more easily than by doing the integral. It is, of course, a false kind of easiness—it has taken you some time to be able to understand Gauss’ law, so you may think that no time has really been saved. But after you have used the theorem more and more, it begins to pay. It is a question of efficiency.
4–8Field lines; equipotential surfaces
We would like now to give a geometrical description of the electrostatic field. The two laws of electrostatics, one that the flux is proportional to the charge inside and the other that the electric field is the gradient of a potential, can also be represented geometrically. We illustrate this with two examples.
First, we take the field of a point charge. We draw lines in the direction of the field—lines which are always tangent to the field, as in Fig. 4-12. These are called field lines. The lines show everywhere the direction of the electric vector. But we also wish to represent the magnitude of the vector. We can make the rule that the strength of the electric field will be represented by the “density” of the lines. By the density of the lines we mean the number of lines per unit area through a surface perpendicular to the lines. With these two rules we can have a picture of the electric field. For a point charge, the density of the lines must decrease as $1/r^2$. But the area of a spherical surface perpendicular to the lines at any radius $r$ increases as $r^2$, so if we always keep the same number of lines for all distances from the charge, the density will remain in proportion to the magnitude of the field. We can guarantee that there are the same number of lines at every distance if we insist that the lines be continuous—that once a line is started from the charge, it never stops. In terms of the field lines, Gauss’ law says that lines should start only at plus charges and stop at minus charges. The number which leave a charge $q$ must be equal to $q/\epsO$.
Now, we can find a similar geometrical picture for the potential $\phi$. The easiest way to represent the potential is to draw surfaces on which $\phi$ is a constant. We call them equipotential surfaces—surfaces of equal potential. Now what is the geometrical relationship of the equipotential surfaces to the field lines? The electric field is the gradient of the potential. The gradient is in the direction of the most rapid change of the potential, and is therefore perpendicular to an equipotential surface. If $\FLPE$ were not perpendicular to the surface, it would have a component in the surface. The potential would be changing in the surface, but then it wouldn’t be an equipotential. The equipotential surfaces must then be everywhere at right angles to the electric field lines.
For a point charge all by itself, the equipotential surfaces are spheres centered at the charge. We have shown in Fig. 4-12 the intersection of these spheres with a plane through the charge.
As a second example, we consider the field near two equal charges, a positive one and a negative one. To get the field is easy. The field is the superposition of the fields from each of the two charges. So, we can take two pictures like Fig. 4-12 and superimpose them—impossible! Then we would have field lines crossing each other, and that’s not possible, because $\FLPE$ can’t have two directions at the same point. The disadvantage of the field-line picture is now evident. By geometrical arguments it is impossible to analyze in a very simple way where the new lines go. From the two independent pictures, we can’t get the combined picture. The principle of superposition, a simple and deep principle about electric fields, does not have, in the field-line picture, an easy representation.
The field-line picture has its uses, however, so we might still like to draw the picture for a pair of equal (and opposite) charges. If we calculate the fields from Eq. (4.13) and the potentials from (4.24), we can draw the field lines and equipotentials. Figure 4-13 shows the result. But we first had to solve the problem mathematically!
| Quantity | Unit |
| $F$ | newton |
| $Q$ | coulomb |
| $L$ | meter |
| $W$ | joule |
| $\rho\sim Q/L^3$ | coulomb/meter³ |
| $1/\epsO\sim FL^2/Q^2$ | newton·meter²/coulomb² |
| $E\sim F/Q$ | newton/coulomb |
| $\phi\sim W/Q$ | joule/coulomb = volt |
| $E\sim \phi/L$ | volt/meter |
| $1/\epsO\sim EL^2/Q$ | volt·meter/coulomb |