5 Application of Gauss’ Law
Application of Gauss’ Law
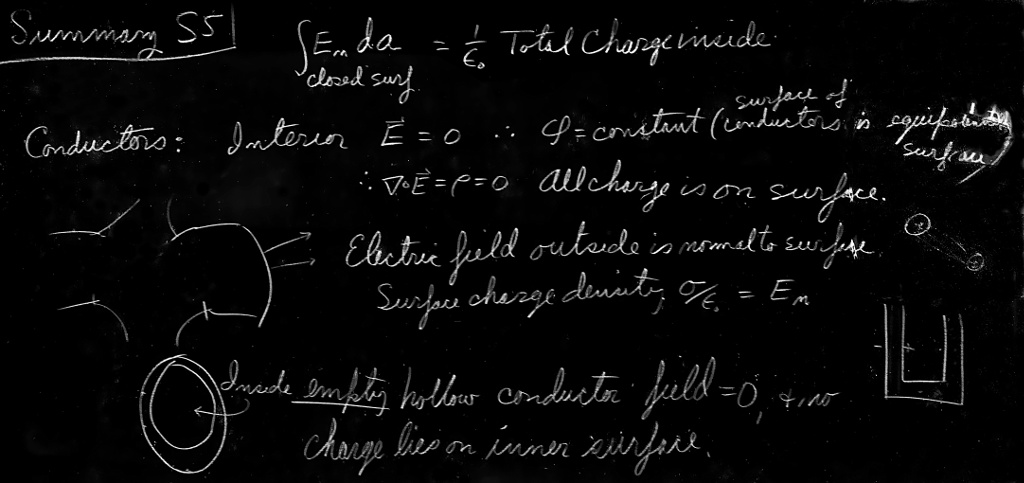
5–1Electrostatics is Gauss’ law plus …
There are two laws of electrostatics: that the flux of the electric field from a volume is proportional to the charge inside—Gauss’ law, and that the circulation of the electric field is zero—$\FLPE$ is a gradient. From these two laws, all the predictions of electrostatics follow. But to say these things mathematically is one thing; to use them easily, and with a certain amount of ingenuity, is another. In this chapter we will work through a number of calculations which can be made with Gauss’ law directly. We will prove theorems and describe some effects, particularly in conductors, that can be understood very easily from Gauss’ law. Gauss’ law by itself cannot give the solution of any problem because the other law must be obeyed too. So when we use Gauss’ law for the solution of particular problems, we will have to add something to it. We will have to presuppose, for instance, some idea of how the field looks—based, for example, on arguments of symmetry. Or we may have to introduce specifically the idea that the field is the gradient of a potential.
5–2Equilibrium in an electrostatic field
Consider first the following question: When can a point charge be in stable mechanical equilibrium in the electric field of other charges? As an example, imagine three negative charges at the corners of an equilateral triangle in a horizontal plane. Would a positive charge placed at the center of the triangle remain there? (It will be simpler if we ignore gravity for the moment, although including it would not change the results.) The force on the positive charge is zero, but is the equilibrium stable? Would the charge return to the equilibrium position if displaced slightly? The answer is no.
There are no points of stable equilibrium in any electrostatic field—except right on top of another charge. Using Gauss’ law, it is easy to see why. First, for a charge to be in equilibrium at any particular point $P_0$, the field must be zero. Second, if the equilibrium is to be a stable one, we require that if we move the charge away from $P_0$ in any direction, there should be a restoring force directed opposite to the displacement. The electric field at all nearby points must be pointing inward—toward the point $P_0$. But that is in violation of Gauss’ law if there is no charge at $P_0$, as we can easily see.
Consider a tiny imaginary surface that encloses $P_0$, as in Fig. 5–1. If the electric field everywhere in the vicinity is pointed toward $P_0$, the surface integral of the normal component is certainly not zero. For the case shown in the figure, the flux through the surface must be a negative number. But Gauss’ law says that the flux of electric field through any surface is proportional to the total charge inside. If there is no charge at $P_0$, the field we have imagined violates Gauss’ law. It is impossible to balance a positive charge in empty space—at a point where there is not some negative charge. A positive charge can be in equilibrium if it is in the middle of a distributed negative charge. Of course, the negative charge distribution would have to be held in place by other than electrical forces!
Our result has been obtained for a point charge. Does the same conclusion hold for a complicated arrangement of charges held together in fixed relative positions—with rods, for example? We consider the question for two equal charges fixed on a rod. Is it possible that this combination can be in equilibrium in some electrostatic field? The answer is again no. The total force on the rod cannot be restoring for displacements in every direction.
Call $\FLPF$ the total force on the rod in any position—$\FLPF$ is then a vector field. Following the argument used above, we conclude that at a position of stable equilibrium, the divergence of $\FLPF$ must be a negative number. But the total force on the rod is the first charge times the field at its position, plus the second charge times the field at its position: \begin{equation} \label{Eq:II:5:1} \FLPF=q_1\FLPE_1+q_2\FLPE_2. \end{equation} The divergence of $\FLPF$ is given by \begin{equation*} \FLPdiv{\FLPF}=q_1(\FLPdiv{\FLPE_1})+q_2(\FLPdiv{\FLPE_2}). \end{equation*} If each of the two charges $q_1$ and $q_2$ is in free space, both $\FLPdiv{\FLPE_1}$ and $\FLPdiv{\FLPE_2}$ are zero, and $\FLPdiv{\FLPF}$ is zero—not negative, as would be required for equilibrium. You can see that an extension of the argument shows that no rigid combination of any number of charges can have a position of stable equilibrium in an electrostatic field in free space.
Now we have not shown that equilibrium is forbidden if there are pivots or other mechanical constraints. As an example, consider a hollow tube in which a charge can move back and forth freely, but not sideways. Now it is very easy to devise an electric field that points inward at both ends of the tube if it is allowed that the field may point laterally outward near the center of the tube. We simply place positive charges at each end of the tube, as in Fig. 5–2. There can now be an equilibrium point even though the divergence of $\FLPE$ is zero. The charge, of course, would not be in stable equilibrium for sideways motion were it not for “nonelectrical” forces from the tube walls.
5–3Equilibrium with conductors
There is no stable spot in the field of a system of fixed charges. What about a system of charged conductors? Can a system of charged conductors produce a field that will have a stable equilibrium point for a point charge? (We mean at a point other than on a conductor, of course.) You know that conductors have the property that charges can move freely around in them. Perhaps when the point charge is displaced slightly, the other charges on the conductors will move in a way that will give a restoring force to the point charge? The answer is still no—although the proof we have just given doesn’t show it. The proof for this case is more difficult, and we will only indicate how it goes.
First, we note that when charges redistribute themselves on the conductors, they can only do so if their motion decreases their total potential energy. (Some energy is lost to heat as they move in the conductor.) Now we have already shown that if the charges producing a field are stationary, there is, near any zero point $P_0$ in the field, some direction for which moving a point charge away from $P_0$ will decrease the energy of the system (since the force is away from $P_0$). Any readjustment of the charges on the conductors can only lower the potential energy still more, so (by the principle of virtual work) their motion will only increase the force in that particular direction away from $P_0$, and not reverse it.
Our conclusions do not mean that it is not possible to balance a charge by electrical forces. It is possible if one is willing to control the locations or the sizes of the supporting charges with suitable devices. You know that a rod standing on its point in a gravitational field is unstable, but this does not prove that it cannot be balanced on the end of a finger. Similarly, a charge can be held in one spot by electric fields if they are variable. But not with a passive—that is, a static—system.
5–4Stability of atoms
If charges cannot be held stably in position, it is surely not proper to imagine matter to be made up of static point charges (electrons and protons) governed only by the laws of electrostatics. Such a static configuration is impossible; it would collapse!
It was once suggested that the positive charge of an atom could be distributed uniformly in a sphere, and the negative charges, the electrons, could be at rest inside the positive charge, as shown in Fig. 5–3. This was the first atomic model, proposed by Thomson. But Rutherford concluded from the experiment of Geiger and Marsden that the positive charges were very much concentrated, in what he called the nucleus. Thomson’s static model had to be abandoned. Rutherford and Bohr then suggested that the equilibrium might be dynamic, with the electrons revolving in orbits, as shown in Fig. 5–4. The electrons would be kept from falling in toward the nucleus by their orbital motion. We already know at least one difficulty with this picture. With such motion, the electrons would be accelerating (because of the circular motion) and would, therefore, be radiating energy. They would lose the kinetic energy required to stay in orbit, and would spiral in toward the nucleus. Again unstable!
The stability of the atoms is now explained in terms of quantum mechanics. The electrostatic forces pull the electron as close to the nucleus as possible, but the electron is compelled to stay spread out in space over a distance given by the uncertainty principle. If it were confined in too small a space, it would have a great uncertainty in momentum. But that means that it would have a high expected energy—which it would use to escape from the electrical attraction. The net result is an electrical equilibrium not too different from the idea of Thomson—only it is the negative charge that is spread out (because the mass of the electron is so much smaller than the mass of the proton).
5–5The field of a line charge
Gauss’ law can be used to solve a number of electrostatic field problems involving a special symmetry—usually spherical, cylindrical, or planar symmetry. In the remainder of this chapter we will apply Gauss’ law to a few such problems. The ease with which these problems can be solved may give the misleading impression that the method is very powerful, and that one should be able to go on to many other problems. It is unfortunately not so. One soon exhausts the list of problems that can be solved easily with Gauss’ law. In later chapters we will develop more powerful methods for investigating electrostatic fields.
As our first example, we consider a system with cylindrical symmetry. Suppose that we have a very long, uniformly charged rod. By this we mean that electric charges are distributed uniformly along an indefinitely long straight line, with the charge $\lambda$ per unit length. We wish to know the electric field. The problem can, of course, be solved by integrating the contribution to the field from every part of the line. We are going to do it without integrating, by using Gauss’ law and some guesswork. First, we surmise that the electric field will be directed radially outward from the line. Any axial component from charges on one side would be accompanied by an equal axial component from charges on the other side. The result could only be a radial field. It also seems reasonable that the field should have the same magnitude at all points equidistant from the line. This is obvious. (It may not be easy to prove, but it is true if space is symmetric—as we believe it is.)
We can use Gauss’ law in the following way. We consider an imaginary surface in the shape of a cylinder coaxial with the line, as shown in Fig. 5–5. According to Gauss’ law, the total flux of $\FLPE$ from this surface is equal to the charge inside divided by $\epsO$. Since the field is assumed to be normal to the surface, the normal component is the magnitude of the field. Let’s call it $E$. Also, let the radius of the cylinder be $r$, and its length be taken as one unit, for convenience. The flux through the cylindrical surface is equal to $E$ times the area of the surface, which is $2\pi r$. The flux through the two end faces is zero because the electric field is tangential to them. The total charge inside our surface is just $\lambda$, because the length of the line inside is one unit. Gauss’ law then gives \begin{gather} E\cdot2\pi r=\lambda/\epsO,\notag\\[1ex] \label{Eq:II:5:2} E=\frac{\lambda}{2\pi\epsO r}. \end{gather} The electric field of a line charge depends inversely on the first power of the distance from the line.
5–6A sheet of charge; two sheets
As another example, we will calculate the field from a uniform plane sheet of charge. Suppose that the sheet is infinite in extent and that the charge per unit area is $\sigma$. We are going to take another guess. Considerations of symmetry lead us to believe that the field direction is everywhere normal to the plane, and if we have no field from any other charges in the world, the fields must be the same (in magnitude) on each side. This time we choose for our Gaussian surface a rectangular box that cuts through the sheet, as shown in Fig. 5–6. The two faces parallel to the sheet will have equal areas, say $A$. The field is normal to these two faces, and parallel to the other four. The total flux is $E$ times the area of the first face, plus $E$ times the area of the opposite face—with no contribution from the other four faces. The total charge enclosed in the box is $\sigma A$. Equating the flux to the charge inside, we have \begin{equation} EA+EA=\frac{\sigma A}{\epsO},\notag \end{equation} from which \begin{equation} \label{Eq:II:5:3} E=\frac{\sigma}{2\epsO}, \end{equation} a simple but important result.
You may remember that the same result was obtained in an earlier chapter by an integration over the entire surface. Gauss’ law gives us the answer, in this instance, much more quickly (although it is not as generally applicable as the earlier method).
We emphasize that this result applies only to the field due to the charges on the sheet. If there are other charges in the neighborhood, the total field near the sheet would be the sum of (5.3) and the field of the other charges. Gauss’ law would then tell us only that \begin{equation} \label{Eq:II:5:4} E_1+E_2=\frac{\sigma}{\epsO}, \end{equation} where $E_1$ and $E_2$ are the fields directed outward on each side of the sheet.
The problem of two parallel sheets with equal and opposite charge densities, $+\sigma$ and $-\sigma$, is equally simple if we assume again that the outside world is quite symmetric. Either by superposing two solutions for a single sheet or by constructing a Gaussian box that includes both sheets, it is easily seen that the field is zero outside of the two sheets (Fig. 5–7a). By considering a box that includes only one surface or the other, as in (b) or (c) of the figure, it can be seen that the field between the sheets must be twice what it is for a single sheet. The result is \begin{alignat}{2} \label{Eq:II:5:5} &E\,(\text{between the sheets})&\,=&\,\sigma/\epsO,\\[2ex] \label{Eq:II:5:6} &E\,(\text{outside}) &\,=&\,0. \end{alignat}
5–7A sphere of charge; a spherical shell
We have already (in Chapter 4) used Gauss’ law to find the field outside a uniformly charged spherical region. The same method can also give us the field at points inside the sphere. For example, the computation can be used to obtain a good approximation to the field inside an atomic nucleus. In spite of the fact that the protons in a nucleus repel each other, they are, because of the strong nuclear forces, spread nearly uniformly throughout the body of the nucleus.
Suppose that we have a sphere of radius $R$ filled uniformly with charge. Let $\rho$ be the charge per unit volume. Again using arguments of symmetry, we assume the field to be radial and equal in magnitude at all points at the same distance from the center. To find the field at the distance $r$ from the center, we take a spherical Gaussian surface of radius $r$ ($r<R$), as shown in Fig. 5–8. The flux out of this surface is \begin{equation*} 4\pi r^2E. \end{equation*} The charge inside our Gaussian surface is the volume inside times $\rho$, or \begin{equation*} \tfrac{4}{3}\pi r^3\rho. \end{equation*} Using Gauss’ law, it follows that the magnitude of the field is given by \begin{equation} \label{Eq:II:5:7} E=\frac{\rho r}{3\epsO}\quad(r<R). \end{equation} You can see that this formula gives the proper result for $r=R$. The electric field is proportional to the radius and is directed radially outward.
The arguments we have just given for a uniformly charged sphere can be applied also to a thin spherical shell of charge. Assuming that the field is everywhere radial and is spherically symmetric, one gets immediately from Gauss’ law that the field outside the shell is like that of a point charge, while the field everywhere inside the shell is zero. (A Gaussian surface inside the shell will contain no charge.)
5–8Is the field of a point charge exactly $\boldsymbol{1/r^2}$?
If we look in a little more detail at how the field inside the shell gets to be zero, we can see more clearly why it is that Gauss’ law is true only because the Coulomb force depends exactly on the square of the distance. Consider any point $P$ inside a uniform spherical shell of charge. Imagine a small cone whose apex is at $P$ and which extends to the surface of the sphere, where it cuts out a small surface area $\Delta a_1$, as in Fig. 5–9. An exactly symmetric cone diverging from the opposite side of $P$ would cut out the surface area $\Delta a_2$. If the distances from $P$ to these two elements of area are $r_1$ and $r_2$, the areas are in the ratio \begin{equation*} \frac{\Delta a_2}{\Delta a_1}=\frac{r_2^2}{r_1^2}. \end{equation*} (You can show this by geometry for any point $P$ inside the sphere.)
If the surface of the sphere is uniformly charged, the charge $\Delta q$ on each of the elements of area is proportional to the area, so \begin{equation*} \frac{\Delta q_2}{\Delta q_1}=\frac{\Delta a_2}{\Delta a_1}. \end{equation*} Coulomb’s law then says that the magnitudes of the fields produced at $P$ by these two surface elements are in the ratio \begin{equation*} \frac{E_2}{E_1}=\frac{\Delta q_2/r_2^2}{\Delta q_1/r_1^2}=1. \end{equation*} The fields cancel exactly. Since all parts of the surface can be paired off in the same way, the total field at $P$ is zero. But you can see that it would not be so if the exponent of $r$ in Coulomb’s law were not exactly two.
The validity of Gauss’ law depends upon the inverse square law of Coulomb. If the force law were not exactly the inverse square, it would not be true that the field inside a uniformly charged sphere would be exactly zero. For instance, if the force varied more rapidly, like, say, the inverse cube of $r$, that portion of the surface which is nearer to an interior point would produce a field which is larger than that which is farther away, resulting in a radial inward field for a positive surface charge. These conclusions suggest an elegant way of finding out whether the inverse square law is precisely correct. We need only determine whether or not the field inside of a uniformly charged spherical shell is precisely zero.
It is lucky that such a method exists. It is usually difficult to measure a physical quantity to high precision—a one percent result may not be too difficult, but how would one go about measuring, say, Coulomb’s law to an accuracy of one part in a billion? It is almost certainly not possible with the best available techniques to measure the force between two charged objects with such an accuracy. But by determining only that the electric fields inside a charged sphere are smaller than some value we can make a highly accurate measurement of the correctness of Gauss’ law, and hence of the inverse square dependence of Coulomb’s law. What one does, in effect, is compare the force law to an ideal inverse square. Such comparisons of things that are equal, or nearly so, are usually the bases of the most precise physical measurements.
How shall we observe the field inside a charged sphere? One way is to try to charge an object by touching it to the inside of a spherical conductor. You know that if we touch a small metal ball to a charged object and then touch it to an electrometer the meter will become charged and the pointer will move from zero (Fig. 5–10a). The ball picks up charge because there are electric fields outside the charged sphere that cause charges to run onto (or off) the little ball. If you do the same experiment by touching the little ball to the inside of the charged sphere, you find that no charge is carried to the electrometer. With such an experiment you can easily show that the field inside is, at most, a few percent of the field outside, and that Gauss’ law is at least approximately correct.
It appears that Benjamin Franklin was the first to notice that the field inside a conducting shell is zero. The result seemed strange to him. When he reported his observation to Priestley, the latter suggested that it might be connected with an inverse square law, since it was known that a spherical shell of matter produced no gravitational field inside. But Coulomb didn’t measure the inverse square dependence until 18 years later, and Gauss’ law came even later still.
Gauss’ law has been checked carefully by putting an electrometer inside a large sphere and observing whether any deflections occur when the sphere is charged to a high voltage. A null result is always obtained. Knowing the geometry of the apparatus and the sensitivity of the meter, it is possible to compute the minimum field that would be observed. From this number it is possible to place an upper limit on the deviation of the exponent from two. If we write that the electrostatic force depends on $r^{-2+\epsilon}$, we can place an upper bound on $\epsilon$. By this method Maxwell determined that $\epsilon$ was less than $1/10{,}000$. The experiment was repeated and improved upon in 1936 by Plimpton and Lawton. They found that Coulomb’s exponent differs from two by less than one part in a billion.
Now that brings up an interesting question: How accurate do we know this Coulomb law to be in various circumstances? The experiments we just described measure the dependence of the field on distance for distances of some tens of centimeters. But what about the distances inside an atom—in the hydrogen atom, for instance, where we believe the electron is attracted to the nucleus by the same inverse square law? It is true that quantum mechanics must be used for the mechanical part of the behavior of the electron, but the force is the usual electrostatic one. In the formulation of the problem, the potential energy of an electron must be known as a function of distance from the nucleus, and Coulomb’s law gives a potential which varies inversely with the first power of the distance. How accurately is the exponent known for such small distances? As a result of very careful measurements in 1947 by Lamb and Retherford on the relative positions of the energy levels of hydrogen, we know that the exponent is correct again to one part in a billion on the atomic scale—that is, at distances of the order of one angstrom ($10^{-8}$ centimeter).
The accuracy of the Lamb-Retherford measurement was possible again because of a physical “accident.” Two of the states of a hydrogen atom are expected to have almost identical energies only if the potential varies exactly as $1/r$. A measurement was made of the very slight difference in energies by finding the frequency $\omega$ of the photons that are emitted or absorbed in the transition from one state to the other, using for the energy difference $\Delta E=\hbar\omega$. Computations showed that $\Delta E$ would have been noticeably different from what was observed if the exponent in the force law $1/r^2$ differed from $2$ by as much as one part in a billion.
Is the same exponent correct at still shorter distances? From measurements in nuclear physics it is found that there are electrostatic forces at typical nuclear distances—at about $10^{-13}$ centimeter—and that they still vary approximately as the inverse square. We shall look at some of the evidence in a later chapter. Coulomb’s law is, we know, still valid, at least to some extent, at distances of the order of $10^{-13}$ centimeter.
How about $10^{-14}$ centimeter? This range can be investigated by bombarding protons with very energetic electrons and observing how they are scattered. Results to date seem to indicate that the law fails at these distances. The electrical force seems to be about $10$ times too weak at distances less than $10^{-14}$ centimeter. Now there are two possible explanations. One is that the Coulomb law does not work at such small distances; the other is that our objects, the electrons and protons, are not point charges. Perhaps either the electron or proton, or both, is some kind of a smear. Most physicists prefer to think that the charge of the proton is smeared. We know that protons interact strongly with mesons. This implies that a proton will, from time to time, exist as a neutron with a $\pi^+$ meson around it. Such a configuration would act—on the average—like a little sphere of positive charge. We know that the field from a sphere of charge does not vary as $1/r^2$ all the way into the center. It is quite likely that the proton charge is smeared, but the theory of pions is still quite incomplete, so it may also be that Coulomb’s law fails at very small distances. The question is still open.
One more point: The inverse square law is valid at distances like one meter and also at $10^{-10}$ m; but is the coefficient $1/4\pi\epsO$ the same? The answer is yes; at least to an accuracy of $15$ parts in a million.
We go back now to an important matter that we slighted when we spoke of the experimental verification of Gauss’ law. You may have wondered how the experiment of Maxwell or of Plimpton and Lawton could give such an accuracy unless the spherical conductor they used was a perfect sphere. An accuracy of one part in a billion is really something to achieve, and you might well ask whether they could make a sphere which was that precise. There are certain to be slight irregularities in any real sphere and if there are irregularities, will they not produce fields inside? We wish to show now that it is not necessary to have a perfect sphere. It is possible, in fact, to show that there is no field inside a closed conducting shell of any shape. In other words, the experiments depended on $1/r^2$, but had nothing to do with the surface being a sphere (except that with a sphere it is easier to calculate what the fields would be if Coulomb had been wrong), so we take up that subject now. To show this, it is necessary to know some of the properties of electrical conductors.
5–9The fields of a conductor
An electrical conductor is a solid that contains many “free” electrons. The electrons can move around freely in the material, but cannot leave the surface. In a metal there are so many free electrons that any electric field will set large numbers of them into motion. Either the current of electrons so set up must be continually kept moving by external sources of energy, or the motion of the electrons will cease as they discharge the sources producing the initial field. In “electrostatic” situations, we do not consider continuous sources of current (they will be considered later when we study magnetostatics), so the electrons move only until they have arranged themselves to produce zero electric field everywhere inside the conductor. (This usually happens in a small fraction of a second.) If there were any field left, this field would urge still more electrons to move; the only electrostatic solution is that the field is everywhere zero inside.
Now consider the interior of a charged conducting object. (By “interior” we mean in the metal itself.) Since the metal is a conductor, the interior field must be zero, and so the gradient of the potential $\phi$ is zero. That means that $\phi$ does not vary from point to point. Every conductor is an equipotential region, and its surface is an equipotential surface. Since in a conducting material the electric field is everywhere zero, the divergence of $\FLPE$ is zero, and by Gauss’ law the charge density in the interior of the conductor must be zero.
If there can be no charges in a conductor, how can it ever be charged? What do we mean when we say a conductor is “charged”? Where are the charges? The answer is that they reside at the surface of the conductor, where there are strong forces to keep them from leaving—they are not completely “free.” When we study solid-state physics, we shall find that the excess charge of any conductor is on the average within one or two atomic layers of the surface. For our present purposes, it is accurate enough to say that if any charge is put on, or in, a conductor it all accumulates on the surface; there is no charge in the interior of a conductor.
We note also that the electric field just outside the surface of a conductor must be normal to the surface. There can be no tangential component. If there were a tangential component, the electrons would move along the surface; there are no forces preventing that. Saying it another way: we know that the electric field lines must always go at right angles to an equipotential surface.
We can also, using Gauss’ law, relate the field strength just outside
a conductor to the local density of the charge at the surface. For a
Gaussian surface, we take a small cylindrical box half inside and half
outside the surface, like the one shown in Fig. 5–11. There
is a contribution to the total flux of $\FLPE$ only from the side of the
box outside the conductor. The field just outside the surface of a
conductor is then
Outside a conductor:
\begin{equation}
\label{Eq:II:5:8}
E=\frac{\sigma}{\epsO},
\end{equation}
where $\sigma$ is the local surface charge density.
Why does a sheet of charge on a conductor produce a different field than just a sheet of charge? In other words, why is (5.8) twice as large as (5.3)? The reason, of course, is that we have not said for the conductor that there are no “other” charges around. There must, in fact, be some to make $\FLPE=\FLPzero$ in the conductor. The charges in the immediate neighborhood of a point $P$ on the surface do, in fact, give a field $E_{\text{local}}=\sigma_{\text{local}}/2\epsO$ both inside and outside the surface. But all the rest of the charges on the conductor “conspire” to produce an additional field at the point $P$ equal in magnitude to $E_{\text{local}}$. The total field inside goes to zero and the field outside to $2E_{\text{local}}=\sigma/\epsO$.
5–10The field in a cavity of a conductor
We return now to the problem of the hollow container—a conductor with a cavity. There is no field in the metal, but what about in the cavity? We shall show that if the cavity is empty then there are no fields in it, no matter what the shape of the conductor or the cavity—say for the one in Fig. 5–12. Consider a Gaussian surface, like $S$ in Fig. 5–12, that encloses the cavity but stays everywhere in the conducting material. Everywhere on $S$ the field is zero, so there is no flux through $S$ and the total charge inside $S$ is zero. For a spherical shell, one could then argue from symmetry that there could be no charge inside. But, in general, we can only say that there are equal amounts of positive and negative charge on the inner surface of the conductor. There could be a positive surface charge on one part and a negative one somewhere else, as indicated in Fig. 5–12. Such a thing cannot be ruled out by Gauss’ law.
What really happens, of course, is that any equal and opposite charges on the inner surface would slide around to meet each other, cancelling out completely. We can show that they must cancel completely by using the law that the circulation of $\FLPE$ is always zero (electrostatics). Suppose there were charges on some parts of the inner surface. We know that there would have to be an equal number of opposite charges somewhere else. Now any lines of $\FLPE$ would have to start on the positive charges and end on the negative charges (since we are considering only the case that there are no free charges in the cavity). Now imagine a loop $\Gamma$ that crosses the cavity along a line of force from some positive charge to some negative charge, and returns to its starting point via the conductor (as in Fig. 5–12). The integral along such a line of force from the positive to the negative charges would not be zero. The integral through the metal is zero, since $\FLPE=\FLPzero$. So we would have \begin{equation*} \oint\FLPE\cdot d\FLPs\neq0??? \end{equation*} But the line integral of $\FLPE$ around any closed loop in an electrostatic field is always zero. So there can be no fields inside the empty cavity, nor any charges on the inside surface.
You should notice carefully one important qualification we have made. We have always said “inside an empty” cavity. If some charges are placed at some fixed locations in the cavity—as on an insulator or on a small conductor insulated from the main one—then there can be fields in the cavity. But then that is not an “empty” cavity.
We have shown that if a cavity is completely enclosed by a conductor, no static distribution of charges outside can ever produce any fields inside. This explains the principle of “shielding” electrical equipment by placing it in a metal can. The same arguments can be used to show that no static distribution of charges inside a closed grounded conductor can produce any fields outside. Shielding works both ways! In electrostatics—but not in varying fields—the fields on the two sides of a closed grounded conducting shell are completely independent.
Now you see why it was possible to check Coulomb’s law to such a great precision. The shape of the hollow shell used doesn’t matter. It doesn’t need to be spherical; it could be square! If Gauss’ law is exact, the field inside is always zero. Now you also understand why it is safe to sit inside the high-voltage terminal of a million-volt Van de Graaff generator, without worrying about getting a shock—because of Gauss’ law.