4 Identical Particles
Identical Particles
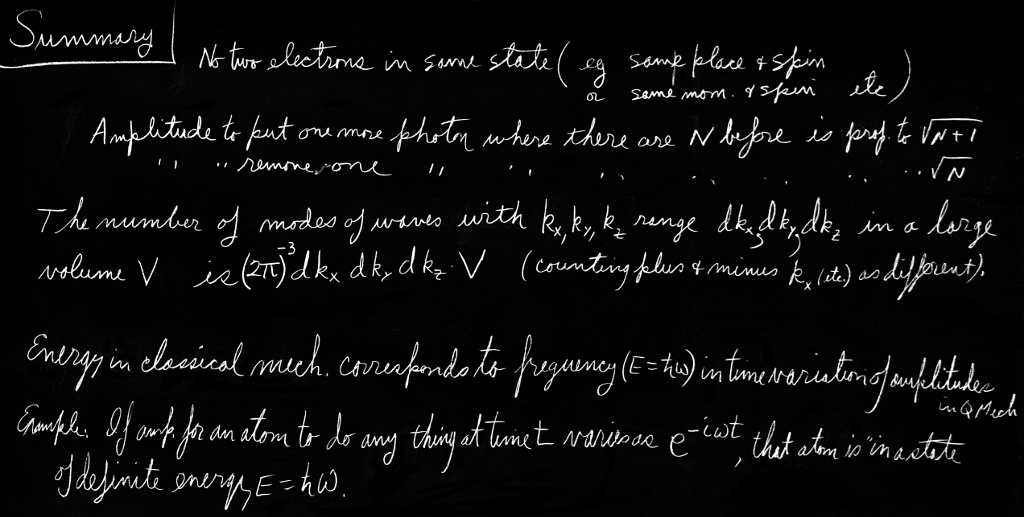
| Review: | Blackbody radiation in: Chapter 41, Vol. I, The Brownian Movement |
| Chapter 42,Vol. I, Applications of Kinetic Theory |
4–1Bose particles and Fermi particles
In the last chapter we began to consider the special rules for the interference that occurs in processes with two identical particles. By identical particles we mean things like electrons which can in no way be distinguished one from another. If a process involves two particles that are identical, reversing which one arrives at a counter is an alternative which cannot be distinguished and—like all cases of alternatives which cannot be distinguished—interferes with the original, unexchanged case. The amplitude for an event is then the sum of the two interfering amplitudes; but, interestingly enough, the interference is in some cases with the same phase and, in others, with the opposite phase.
Suppose we have a collision of two particles $a$ and $b$ in which particle $a$ scatters in the direction $1$ and particle $b$ scatters in the direction $2$, as sketched in Fig. 4–1(a). Let’s call $f(\theta)$ the amplitude for this process; then the probability $P_1$ of observing such an event is proportional to $\abs{f(\theta)}^2$. Of course, it could also happen that particle $b$ scattered into counter $1$ and particle $a$ went into counter $2$, as shown in Fig. 4–1(b). Assuming that there are no special directions defined by spins or such, the probability $P_2$ for this process is just $\abs{f(\pi-\theta)}^2$, because it is just equivalent to the first process with counter $1$ moved over to the angle $\pi-\theta$. You might also think that the amplitude for the second process is just $f(\pi-\theta)$. But that is not necessarily so, because there could be an arbitrary phase factor. That is, the amplitude could be \begin{equation*} e^{i\delta}f(\pi-\theta). \end{equation*} Such an amplitude still gives a probability $P_2$ equal to $\abs{f(\pi-\theta)}^2$.
Now let’s see what happens if $a$ and $b$ are identical
particles. Then the two different processes shown in the two diagrams
of Fig. 4–1 cannot be distinguished. There is an amplitude that
either $a$ or $b$ goes into counter $1$, while the other goes
into counter $2$. This amplitude is the sum of the amplitudes for the
two processes shown in Fig. 4–1. If we call the first
one $f(\theta)$, then the second one is $e^{i\delta}f(\pi-\theta)$, where
now the phase factor is very important because we are going to be
adding two amplitudes. Suppose we have to multiply the amplitude by a
certain phase factor when we exchange the roles of the two
particles. If we exchange them again we should get the same factor
again. But we are then back to the first process. The phase factor
taken twice must bring us back where we started—its square must be
equal to $1$. There are only two possibilities: $e^{i\delta}$ is equal
to $+1$, or is equal to $-1$. Either the exchanged case contributes
with the same sign, or it contributes with the opposite
sign. Both cases exist in nature, each for a different class of
particles. Particles which interfere with a positive sign are
called Bose particles and those which interfere with a
negative sign are called Fermi particles. The Bose
particles are the photon, the mesons, and the graviton. The Fermi
particles are the electron, the muon, the neutrinos, the nucleons, and
the baryons. We have, then, that the amplitude for the scattering of
identical particles is:
Bose particles:
\begin{equation}
\label{Eq:III:4:1}
(\text{Amplitude direct})+(\text{Amplitude exchanged}).
\end{equation}
Fermi particles:
\begin{equation}
\label{Eq:III:4:2}
(\text{Amplitude direct})-(\text{Amplitude exchanged}).
\end{equation}
For particles with spin—like electrons—there is an additional complication. We must specify not only the location of the particles but the direction of their spins. It is only for identical particles with identical spin states that the amplitudes interfere when the particles are exchanged. If you think of the scattering of unpolarized beams—which are a mixture of different spin states—there is some extra arithmetic.
Now an interesting problem arises when there are two or more particles bound tightly together. For example, an $\alpha$-particle has four particles in it—two neutrons and two protons. When two $\alpha$-particles scatter, there are several possibilities. It may be that during the scattering there is a certain amplitude that one of the neutrons will leap across from one $\alpha$-particle to the other, while a neutron from the other $\alpha$-particle leaps the other way so that the two alphas which come out of the scattering are not the original ones—there has been an exchange of a pair of neutrons. See Fig. 4–2. The amplitude for scattering with an exchange of a pair of neutrons will interfere with the amplitude for scattering with no such exchange, and the interference must be with a minus sign because there has been an exchange of one pair of Fermi particles. On the other hand, if the relative energy of the two $\alpha$-particles is so low that they stay fairly far apart—say, due to the Coulomb repulsion—and there is never any appreciable probability of exchanging any of the internal particles, we can consider the $\alpha$-particle as a simple object, and we do not need to worry about its internal details. In such circumstances, there are only two contributions to the scattering amplitude. Either there is no exchange, or all four of the nucleons are exchanged in the scattering. Since the protons and the neutrons in the $\alpha$-particle are all Fermi particles, an exchange of any pair reverses the sign of the scattering amplitude. So long as there are no internal changes in the $\alpha$-particles, interchanging the two $\alpha$-particles is the same as interchanging four pairs of Fermi particles. There is a change in sign for each pair, so the net result is that the amplitudes combine with a positive sign. The $\alpha$-particle behaves like a Bose particle.
So the rule is that composite objects, in circumstances in which the composite object can be considered as a single object, behave like Fermi particles or Bose particles, depending on whether they contain an odd number or an even number of Fermi particles.
All the elementary Fermi particles we have mentioned—such as the electron, the proton, the neutron, and so on—have a spin $j=1/2$. If several such Fermi particles are put together to form a composite object, the resulting spin may be either integral or half-integral. For example, the common isotope of helium, He$^4$, which has two neutrons and two protons, has a spin of zero, whereas Li$^7$, which has three protons and four neutrons, has a spin of $3/2$. We will learn later the rules for compounding angular momentum, and will just mention now that every composite object which has a half-integral spin imitates a Fermi particle, whereas every composite object with an integral spin imitates a Bose particle.
This brings up an interesting question: Why is it that particles with half-integral spin are Fermi particles whose amplitudes add with the minus sign, whereas particles with integral spin are Bose particles whose amplitudes add with the positive sign? We apologize for the fact that we cannot give you an elementary explanation. An explanation has been worked out by Pauli from complicated arguments of quantum field theory and relativity. He has shown that the two must necessarily go together, but we have not been able to find a way of reproducing his arguments on an elementary level. It appears to be one of the few places in physics where there is a rule which can be stated very simply, but for which no one has found a simple and easy explanation. The explanation is deep down in relativistic quantum mechanics. This probably means that we do not have a complete understanding of the fundamental principle involved. For the moment, you will just have to take it as one of the rules of the world.
4–2States with two Bose particles
Now we would like to discuss an interesting consequence of the addition rule for Bose particles. It has to do with their behavior when there are several particles present. We begin by considering a situation in which two Bose particles are scattered from two different scatterers. We won’t worry about the details of the scattering mechanism. We are interested only in what happens to the scattered particles. Suppose we have the situation shown in Fig. 4–3. The particle $a$ is scattered into the state $1$. By a state we mean a given direction and energy, or some other given condition. The particle $b$ is scattered into the state $2$. We want to assume that the two states $1$ and $2$ are nearly the same. (What we really want to find out eventually is the amplitude that the two particles are scattered into identical directions, or states; but it is best if we think first about what happens if the states are almost the same and then work out what happens when they become identical.)
Suppose that we had only particle $a$; then it would have a certain amplitude for scattering in direction $1$, say $\braket{1}{a}$. And particle $b$ alone would have the amplitude $\braket{2}{b}$ for landing in direction $2$. If the two particles are not identical, the amplitude for the two scatterings to occur at the same time is just the product \begin{equation*} \braket{1}{a}\braket{2}{b}. \end{equation*} The probability for such an event is then \begin{equation*} \abs{\braket{1}{a}\braket{2}{b}}^2, \end{equation*} which is also equal to \begin{equation*} \abs{\braket{1}{a}}^2\abs{\braket{2}{b}}^2. \end{equation*} To save writing for the present arguments, we will sometimes set \begin{equation*} \braket{1}{a}=a_1,\quad \braket{2}{b}=b_2. \end{equation*} Then the probability of the double scattering is \begin{equation*} \abs{a_1}^2\abs{b_2}^2. \end{equation*}
It could also happen that particle $b$ is scattered into direction $1$, while particle $a$ goes into direction $2$. The amplitude for this process is \begin{equation*} \braket{2}{a}\braket{1}{b}, \end{equation*} and the probability of such an event is \begin{equation*} \abs{\braket{2}{a}\braket{1}{b}}^2= \abs{a_2}^2\abs{b_1}^2. \end{equation*}
Imagine now that we have a pair of tiny counters that pick up the two scattered particles. The probability $P_2$ that they will pick up two particles together is just the sum \begin{equation} \label{Eq:III:4:3} P_2=\abs{a_1}^2\abs{b_2}^2+\abs{a_2}^2\abs{b_1}^2. \end{equation}
Now let’s suppose that the directions $1$ and $2$ are very close together. We expect that $a$ should vary smoothly with direction, so $a_1$ and $a_2$ must approach each other as $1$ and $2$ get close together. If they are close enough, the amplitudes $a_1$ and $a_2$ will be equal. We can set $a_1=a_2$ and call them both just $a$; similarly, we set $b_1=b_2=b$. Then we get that \begin{equation} \label{Eq:III:4:4} P_2=2\abs{a}^2\abs{b}^2. \end{equation}
Now suppose, however, that $a$ and $b$ are identical Bose particles. Then the process of $a$ going into $1$ and $b$ going into $2$ cannot be distinguished from the exchanged process in which $a$ goes into $2$ and $b$ goes into $1$. In this case the amplitudes for the two different processes can interfere. The total amplitude to obtain a particle in each of the two counters is \begin{equation} \label{Eq:III:4:5} \braket{1}{a}\braket{2}{b}+\braket{2}{a}\braket{1}{b}. \end{equation} And the probability that we get a pair is the absolute square of this amplitude, \begin{equation} \label{Eq:III:4:6} P_2=\abs{a_1b_2+a_2b_1}^2=4\abs{a}^2\abs{b}^2. \end{equation} We have the result that it is twice as likely to find two identical Bose particles scattered into the same state as you would calculate assuming the particles were different.
Although we have been considering that the two particles are observed in separate counters, this is not essential—as we can see in the following way. Let’s imagine that both the directions $1$ and $2$ would bring the particles into a single small counter which is some distance away. We will let the direction $1$ be defined by saying that it heads toward the element of area $dS_1$ of the counter. Direction $2$ heads toward the surface element $dS_2$ of the counter. (We imagine that the counter presents a surface at right angles to the line from the scatterings.) Now we cannot give a probability that a particle will go into a precise direction or to a particular point in space. Such a thing is impossible—the chance for any exact direction is zero. When we want to be so specific, we shall have to define our amplitudes so that they give the probability of arriving per unit area of a counter. Suppose that we had only particle $a$; it would have a certain amplitude for scattering in direction $1$. Let’s define $\braket{1}{a}=a_1$ to be the amplitude that $a$ will scatter into a unit area of the counter in the direction $1$. In other words, the scale of $a_1$ is chosen—we say it is “normalized” so that the probability that it will scatter into an element of area $dS_1$ is \begin{equation} \label{Eq:III:4:7} \abs{\braket{1}{a}}^2\,dS_1=\abs{a_1}^2\,dS_1. \end{equation} If our counter has the total area $\Delta S$, and we let $dS_1$ range over this area, the total probability that the particle $a$ will be scattered into the counter is \begin{equation} \label{Eq:III:4:8} \int_{\Delta S}\abs{a_1}^2\,dS_1. \end{equation}
As before, we want to assume that the counter is sufficiently small so that the amplitude $a_1$ doesn’t vary significantly over the surface of the counter; $a_1$ is then a constant amplitude which we can call $a$. Then the probability that particle $a$ is scattered somewhere into the counter is \begin{equation} \label{Eq:III:4:9} p_a=\abs{a}^2\,\Delta S. \end{equation}
In the same way, we will have that the probability that particle $b$—when it is alone—scatters into some element of area, say $dS_2$, is \begin{equation*} \abs{b_2}^2\,dS_2. \end{equation*} (We use $dS_2$ instead of $dS_1$ because we will later want $a$ and $b$ to go into different directions.) Again we set $b_2$ equal to the constant amplitude $b$; then the probability that particle $b$ is counted in the detector is \begin{equation} \label{Eq:III:4:10} p_b=\abs{b}^2\,\Delta S. \end{equation}
Now when both particles are present, the probability that $a$ is scattered into $dS_1$ and $b$ is scattered into $dS_2$ is \begin{equation} \label{Eq:III:4:11} \abs{a_1b_2}^2\,dS_1\,dS_2=\abs{a}^2\abs{b}^2\,dS_1\,dS_2. \end{equation} If we want the probability that both $a$ and $b$ get into the counter, we integrate both $dS_1$ and $dS_2$ over $\Delta S$ and find that \begin{equation} \label{Eq:III:4:12} P_2=\abs{a}^2\abs{b}^2\,(\Delta S)^2. \end{equation} We notice, incidentally, that this is just equal to $p_a\cdot p_b$, just as you would suppose assuming that the particles $a$ and $b$ act independently of each other.
When the two particles are identical, however, there are two indistinguishable possibilities for each pair of surface elements $dS_1$ and $dS_2$. Particle $a$ going into $dS_2$ and particle $b$ going into $dS_1$ is indistinguishable from $a$ into $dS_1$ and $b$ into $dS_2$, so the amplitudes for these processes will interfere. (When we had two different particles above—although we did not in fact care which particle went where in the counter—we could, in principle, have found out; so there was no interference. For identical particles we cannot tell, even in principle.) We must write, then, that the probability that the two particles arrive at $dS_1$ and $dS_2$ is \begin{equation} \label{Eq:III:4:13} \abs{a_1b_2+a_2b_1}^2\,dS_1\,dS_2. \end{equation} Now, however, when we integrate over the area of the counter, we must be careful. If we let $dS_1$ and $dS_2$ range over the whole area $\Delta S$, we would count each part of the area twice since (4.13) contains everything that can happen with any pair of surface elements $dS_1$ and $dS_2$.1 We can still do the integral that way, if we correct for the double counting by dividing the result by $2$. We get then that $P_2$ for identical Bose particles is \begin{equation} \label{Eq:III:4:14} P_2(\text{Bose})=\tfrac{1}{2}\{4\abs{a}^2\abs{b}^2\,(\Delta S)^2\}= 2\abs{a}^2\abs{b}^2\,(\Delta S)^2. \end{equation} Again, this is just twice what we got in Eq. (4.12) for distinguishable particles.
If we imagine for a moment that we knew that the $b$ channel had already sent its particle into the particular direction, we can say that the probability that a second particle will go into the same direction is twice as great as we would have expected if we had calculated it as an independent event. It is a property of Bose particles that if there is already one particle in a condition of some kind, the probability of getting a second one in the same condition is twice as great as it would be if the first one were not already there. This fact is often stated in the following way: If there is already one Bose particle in a given state, the amplitude for putting an identical one on top of it is $\sqrt{2}$ greater than if it weren’t there. (This is not a proper way of stating the result from the physical point of view we have taken, but if it is used consistently as a rule, it will, of course, give the correct result.)
4–3States with $\boldsymbol{n}$ Bose particles
Let’s extend our result to a situation in which there are $n$ particles present. We imagine the circumstance shown in Fig. 4–4. We have $n$ particles $a$, $b$, $c$, …, which are scattered and end up in the directions $1$, $2$, $3$, …, $n$. All $n$ directions are headed toward a small counter a long distance away. As in the last section, we choose to normalize all the amplitudes so that the probability that each particle acting alone would go into an element of surface $dS$ of the counter is \begin{equation*} \abs{\langle\quad\rangle}^2\,dS. \end{equation*}
First, let’s assume that the particles are all distinguishable; then the probability that $n$ particles will be counted together in $n$ different surface elements is \begin{equation} \label{Eq:III:4:15} \abs{a_1b_2c_3\dotsm}^2\,dS_1\,dS_2\,dS_3\dotsm \end{equation} Again we take that the amplitudes don’t depend on where $dS$ is located in the counter (assumed small) and call them simply $a$, $b$, $c$, … The probability (4.15) becomes \begin{equation} \label{Eq:III:4:16} \abs{a}^2\abs{b}^2\abs{c}^2\dotsm dS_1\,dS_2\,dS_3\dotsm \end{equation} Integrating each $dS$ over the surface $\Delta S$ of the counter, we have that $P_n(\text{different})$, the probability of counting $n$ different particles at once, is \begin{equation} \label{Eq:III:4:17} P_n(\text{different})=\abs{a}^2\abs{b}^2\abs{c}^2\dotsm(\Delta S)^n. \end{equation} This is just the product of the probabilities for each particle to enter the counter separately. They all act independently—the probability for one to enter does not depend on how many others are also entering.
Now suppose that all the particles are identical Bose particles. For each set of directions $1$, $2$, $3$, … there are many indistinguishable possibilities. If there were, for instance, just three particles, we would have the following possibilities: \begin{alignat*}{3} a\!&\to\!1&\quad a\!&\to\!1&\quad a\!&\to\!2\\ b\!&\to\!2&\quad b\!&\to\!3&\quad b\!&\to\!1\\ c\!&\to\!3&\quad c\!&\to\!2&\quad c\!&\to\!3\\[1ex] a\!&\to\!2&\quad a\!&\to\!3&\quad a\!&\to\!3\\ b\!&\to\!3&\quad b\!&\to\!1&\quad b\!&\to\!2\\ c\!&\to\!1&\quad c\!&\to\!2&\quad c\!&\to\!1 \end{alignat*} There are six different combinations. With $n$ particles, there are $n!$ different, but indistinguishable, possibilities for which we must add amplitudes. The probability that $n$ particles will be counted in $n$ surface elements is then \begin{align} \lvert a_1b_2c_3\dotsm&+a_1b_3c_2\dotsm+a_2b_1c_3\dotsm\notag\\ \label{Eq:III:4:18} &+a_2b_3c_1\dotsm+\text{etc.}+\text{etc.}\rvert^2 dS_1\,dS_2\,dS_3\dotsm dS_n. \end{align} Once more we assume that all the directions are so close that we can set $a_1=$ $a_2=$ $\dotsb=$ $a_n=$ $a$, and similarly for $b$, $c$, …; the probability of (4.18) becomes \begin{equation} \label{Eq:III:4:19} \abs{n!abc\dotsm}^2dS_1\,dS_2\dotsm dS_n. \end{equation}
When we integrate each $dS$ over the area $\Delta S$ of the counter, each possible product of surface elements is counted $n!$ times; we correct for this by dividing by $n!$ and get \begin{equation} P_n(\text{Bose}) =\frac{1}{n!}\,\abs{n!abc\dotsm}^2(\Delta S)^n\notag \end{equation} or \begin{equation} \label{Eq:III:4:20} P_n(\text{Bose}) =n!\,\abs{abc\dotsm}^2(\Delta S)^n. \end{equation} Comparing this result with Eq. (4.17), we see that the probability of counting $n$ Bose particles together is $n!$ greater than we would calculate assuming that the particles were all distinguishable. We can summarize our result this way: \begin{equation} \label{Eq:III:4:21} P_n(\text{Bose})=n!\,P_n(\text{different}). \end{equation} Thus, the probability in the Bose case is larger by $n!$ than you would calculate assuming that the particles acted independently.
We can see better what this means if we ask the following question: What is the probability that a Bose particle will go into a particular state when there are already $n$ others present? Let’s call the newly added particle $w$. If we have $(n+1)$ particles, including $w$, Eq. (4.20) becomes \begin{equation} \label{Eq:III:4:22} P_{n+1}(\text{Bose})=(n+1)!\,\abs{abc\dotsm w}^2(\Delta S)^{n+1}. \end{equation} We can write this as \begin{equation} P_{n+1}(\text{Bose})=\{(n+1)\abs{w}^2\,\Delta S\}n!\,\abs{abc\dotsm}^2(\Delta S)^n\notag \end{equation} or \begin{equation} \label{Eq:III:4:23} P_{n+1}(\text{Bose})=(n+1)\abs{w}^2\,\Delta S\,P_n(\text{Bose}). \end{equation}
We can look at this result in the following way: The number $\abs{w}^2\,\Delta S$ is the probability for getting particle $w$ into the detector if no other particles were present; $P_n(\text{Bose})$ is the chance that there are already $n$ other Bose particles present. So Eq. (4.23) says that when there are $n$ other identical Bose particles present, the probability that one more particle will enter the same state is enhanced by the factor $(n+1)$. The probability of getting a boson, where there are already $n$, is $(n+1)$ times stronger than it would be if there were none before. The presence of the other particles increases the probability of getting one more.
4–4Emission and absorption of photons
Throughout our discussion we have talked about a process like the scattering of $\alpha$-particles. But that is not essential; we could have been speaking of the creation of particles, as for instance the emission of light. When the light is emitted, a photon is “created.” In such a case, we don’t need the incoming lines in Fig. 4–4; we can consider merely that there are some atoms emitting $n$ photons, as in Fig. 4–5. So our result can also be stated: The probability that an atom will emit a photon into a particular final state is increased by the factor $(n+1)$ if there are already $n$ photons in that state.
People like to summarize this result by saying that the amplitude to emit a photon is increased by the factor $\sqrt{n+1}$ when there are already $n$ photons present. It is, of course, another way of saying the same thing if it is understood to mean that this amplitude is just to be squared to get the probability.
It is generally true in quantum mechanics that the amplitude to get from any condition $\phi$ to any other condition $\chi$ is the complex conjugate of the amplitude to get from $\chi$ to $\phi$: \begin{equation} \label{Eq:III:4:24} \braket{\chi}{\phi}=\braket{\phi}{\chi}\cconj. \end{equation} We will learn about this law a little later, but for the moment we will just assume it is true. We can use it to find out how photons are scattered or absorbed out of a given state. We have that the amplitude that a photon will be added to some state, say $i$, when there are already $n$ photons present is, say, \begin{equation} \label{Eq:III:4:25} \braket{n+1}{n}=\sqrt{n+1}\,a, \end{equation} where $a=\braket{i}{a}$ is the amplitude when there are no others present. Using Eq. (4.24), the amplitude to go the other way—from $(n+1)$ photons to $n$—is \begin{equation} \label{Eq:III:4:26} \braket{n}{n+1}=\sqrt{n+1}\,a\cconj. \end{equation}
This isn’t the way people usually say it; they don’t like to think of going from $(n+1)$ to $n$, but prefer always to start with $n$ photons present. Then they say that the amplitude to absorb a photon when there are $n$ present—in other words, to go from $n$ to $(n-1)$—is \begin{equation} \label{Eq:III:4:27} \braket{n-1}{n}=\sqrt{n}\,a\cconj. \end{equation} which is, of course, just the same as Eq. (4.26). Then they have trouble trying to remember when to use $\sqrt{n}$ or $\sqrt{n+1}$. Here’s the way to remember: The factor is always the square root of the largest number of photons present, whether it is before or after the reaction. Equations (4.25) and (4.26) show that the law is really symmetric—it only appears unsymmetric if you write it as Eq. (4.27).
There are many physical consequences of these new rules; we want to describe one of them having to do with the emission of light. Suppose we imagine a situation in which photons are contained in a box—you can imagine a box with mirrors for walls. Now say that in the box we have $n$ photons, all of the same state—the same frequency, direction, and polarization—so they can’t be distinguished, and that also there is an atom in the box that can emit another photon into the same state. Then the probability that it will emit a photon is \begin{equation} \label{Eq:III:4:28} (n+1)\abs{a}^2, \end{equation} and the probability that it will absorb a photon is \begin{equation} \label{Eq:III:4:29} n\abs{a}^2, \end{equation} where $\abs{a}^2$ is the probability it would emit if no photons were present. We have already discussed these rules in a somewhat different way in Chapter 42 of Vol. I. Equation (4.29) says that the probability that an atom will absorb a photon and make a transition to a higher energy state is proportional to the intensity of the light shining on it. But, as Einstein first pointed out, the rate at which an atom will make a transition downward has two parts. There is the probability that it will make a spontaneous transition $\abs{a}^2$, plus the probability of an induced transition $n\abs{a}^2$, which is proportional to the intensity of the light—that is, to the number of photons present. Furthermore, as Einstein said, the coefficients of absorption and of induced emission are equal and are related to the probability of spontaneous emission. What we learn here is that if the light intensity is measured in terms of the number of photons present (instead of as the energy per unit area, and per sec), the coefficients of absorption, of induced emission, and of spontaneous emission are all equal. This is the content of the relation between the Einstein coefficients $A$ and $B$ of Chapter 42, Vol. I, Eq. (42.18).
4–5The blackbody spectrum
We would like to use our rules for Bose particles to discuss once more the spectrum of blackbody radiation (see Chapter 42, Vol. I). We will do it by finding out how many photons there are in a box if the radiation is in thermal equilibrium with some atoms in the box. Suppose that for each light frequency $\omega$, there are a certain number $N$ of atoms which have two energy states separated by the energy $\Delta E=\hbar\omega$. See Fig. 4–6. We’ll call the lower-energy state the “ground” state and the upper state the “excited” state. Let $N_g$ and $N_e$ be the average numbers of atoms in the ground and excited states; then in thermal equilibrium at the temperature $T$, we have from statistical mechanics that \begin{equation} \label{Eq:III:4:30} \frac{N_e}{N_g}=e^{-\Delta E/\kappa T}=e^{-\hbar\omega/\kappa T}. \end{equation}
Each atom in the ground state can absorb a photon and go into the excited state, and each atom in the excited state can emit a photon and go to the ground state. In equilibrium, the rates for these two processes must be equal. The rates are proportional to the probability for the event and to the number of atoms present. Let’s let $\overline{n}$ be the average number of photons present in a given state with the frequency $\omega$. Then the absorption rate from that state is $N_g\overline{n}\abs{a}^2$, and the emission rate into that state is $N_e(\overline{n}+1)\abs{a}^2$. Setting the two rates equal, we have that \begin{equation} \label{Eq:III:4:31} N_g\overline{n}=N_e(\overline{n}+1). \end{equation} Combining this with Eq. (4.30), we have \begin{equation} \frac{\overline{n}}{\overline{n}+1}=e^{-\hbar\omega/\kappa T}.\notag \end{equation} Solving for $\overline{n}$, we have \begin{equation} \label{Eq:III:4:32} \overline{n}=\frac{1}{e^{\hbar\omega/\kappa T}-1}, \end{equation} which is the mean number of photons in any state with frequency $\omega$, for a cavity in thermal equilibrium. Since each photon has the energy $\hbar\omega$, the energy in the photons of a given state is $\overline{n}\hbar\omega$, or \begin{equation} \label{Eq:III:4:33} \frac{\hbar\omega}{e^{\hbar\omega/\kappa T}-1}. \end{equation}
Incidentally, we once found a similar equation in another context [Chapter 41, Vol. I, Eq. (41.15)]. You remember that for any harmonic oscillator—such as a weight on a spring—the quantum mechanical energy levels are equally spaced with a separation $\hbar\omega$, as drawn in Fig. 4–7. If we call the energy of the $n$th level $n\hbar\omega$, we find that the mean energy of such an oscillator is also given by Eq. (4.33). Yet this equation was derived here for photons, by counting particles, and it gives the same results. That is one of the marvelous miracles of quantum mechanics. If one begins by considering a kind of state or condition for Bose particles which do not interact with each other (we have assumed that the photons do not interact with each other), and then considers that into this state there can be put either zero, or one, or two, … up to any number $n$ of particles, one finds that this system behaves for all quantum mechanical purposes exactly like a harmonic oscillator. By such an oscillator we mean a dynamic system like a weight on a spring or a standing wave in a resonant cavity. And that is why it is possible to represent the electromagnetic field by photon particles. From one point of view, we can analyze the electromagnetic field in a box or cavity in terms of a lot of harmonic oscillators, treating each mode of oscillation according to quantum mechanics as a harmonic oscillator. From a different point of view, we can analyze the same physics in terms of identical Bose particles. And the results of both ways of working are always in exact agreement. There is no way to make up your mind whether the electromagnetic field is really to be described as a quantized harmonic oscillator or by giving how many photons there are in each condition. The two views turn out to be mathematically identical. So in the future we can speak either about the number of photons in a particular state in a box or the number of the energy level associated with a particular mode of oscillation of the electromagnetic field. They are two ways of saying the same thing. The same is true of photons in free space. They are equivalent to oscillations of a cavity whose walls have receded to infinity.
We have computed the mean energy in any particular mode in a box at the temperature $T$; we need only one more thing to get the blackbody radiation law: We need to know how many modes there are at each energy. (We assume that for every mode there are some atoms in the box—or in the walls—which have energy levels that can radiate into that mode, so that each mode can get into thermal equilibrium.) The blackbody radiation law is usually stated by giving the energy per unit volume carried by the light in a small frequency interval from $\omega$ to $\omega+\Delta\omega$. So we need to know how many modes there are in a box with frequencies in the interval $\Delta\omega$. Although this question continually comes up in quantum mechanics, it is purely a classical question about standing waves.
We will get the answer only for a rectangular box. It comes out the same for a box of any shape, but it’s very complicated to compute for the arbitrary case. Also, we are only interested in a box whose dimensions are very large compared with a wavelength of the light. Then there are billions and billions of modes; there will be many in any small frequency interval $\Delta\omega$, so we can speak of the “average number” in any $\Delta\omega$ at the frequency $\omega$. Let’s start by asking how many modes there are in a one-dimensional case—as for waves on a stretched string. You know that each mode is a sine wave that has to go to zero at both ends; in other words, there must be an integral number of half-wavelengths in the length of the line, as shown in Fig. 4–8. We prefer to use the wave number $k=2\pi/\lambda$; calling $k_j$ the wave number of the $j$th mode, we have that \begin{equation} \label{Eq:III:4:34} k_j=\frac{j\pi}{L}, \end{equation} where $j$ is any integer. The separation $\delta k$ between successive modes is \begin{equation*} \delta k=k_{j+1}-k_j=\frac{\pi}{L}. \end{equation*} We want to assume that $kL$ is so large that in a small interval $\Delta k$, there are many modes. Calling $\Delta\numModes$ the number of modes in the interval $\Delta k$, we have \begin{equation} \label{Eq:III:4:35} \Delta\numModes=\frac{\Delta k}{\delta k}=\frac{L}{\pi}\,\Delta k. \end{equation}
Now theoretical physicists working in quantum mechanics usually prefer to say that there are one-half as many modes; they write \begin{equation} \label{Eq:III:4:36} \Delta\numModes=\frac{L}{2\pi}\,\Delta k. \end{equation} We would like to explain why. They usually like to think in terms of travelling waves—some going to the right (with a positive $k$) and some going to the left (with a negative $k$). But a “mode” is a standing wave which is the sum of two waves, one going in each direction. In other words, they consider each standing wave as containing two distinct photon “states.” So if by $\Delta\numModes$, one prefers to mean the number of photon states of a given $k$ (where now $k$ ranges over positive and negative values), one should then take $\Delta\numModes$ half as big. (All integrals must now go from $k=-\infty$ to $k=+\infty$, and the total number of states up to any given absolute value of $k$ will come out O.K.) Of course, we are not then describing standing waves very well, but we are counting modes in a consistent way.
Now we want to extend the results to three dimensions. A standing wave in a rectangular box must have an integral number of half-waves along each axis. The situation for two of the dimensions is shown in Fig. 4–9. Each wave direction and frequency is described by a vector wave number $\FLPk$, whose $x$, $y$, and $z$ components must satisfy equations like Eq. (4.34). So we have that \begin{align*} k_x&=\frac{j_x\pi}{L_x},\\[.5ex] k_y&=\frac{j_y\pi}{L_y},\\[.5ex] k_z&=\frac{j_z\pi}{L_z}. \end{align*} The number of modes with $k_x$ in an interval $\Delta k_x$ is, as before, \begin{equation*} \frac{L_x}{2\pi}\,\Delta k_x, \end{equation*} and similarly for $\Delta k_y$ and $\Delta k_z$. If we call $\Delta\numModes(\FLPk)$ the number of modes for a vector wave number $\FLPk$ whose $x$-component is between $k_x$ and $k_x+\Delta k_x$, whose $y$-component is between $k_y$ and $k_y+\Delta k_y$, and whose $z$-component is between $k_z$ and $k_z+\Delta k_z$, then \begin{equation} \label{Eq:III:4:37} \Delta\numModes(\FLPk)=\frac{L_xL_yL_z}{(2\pi)^3}\, \Delta k_x\,\Delta k_y\,\Delta k_z. \end{equation} The product $L_xL_yL_z$ is equal to the volume $V$ of the box. So we have the important result that for high frequencies (wavelengths small compared with the dimensions), the number of modes in a cavity is proportional to the volume $V$ of the box and to the “volume in $k$-space” $\Delta k_x\,\Delta k_y\,\Delta k_z$. This result comes up again and again in many problems and should be memorized: \begin{equation} \label{Eq:III:4:38} d\numModes(\FLPk)=V\,\frac{d^3\FLPk}{(2\pi)^3}. \end{equation} Although we have not proved it, the result is independent of the shape of the box.
We will now apply this result to find the number of photon modes for photons with frequencies in the range $\Delta\omega$. We are just interested in the energy in various modes—but not interested in the directions of the waves. We would like to know the number of modes in a given range of frequencies. In a vacuum the magnitude of $\FLPk$ is related to the frequency by \begin{equation} \label{Eq:III:4:39} \abs{\FLPk}=\frac{\omega}{c}. \end{equation} So in a frequency interval $\Delta\omega$, these are all the modes which correspond to $\FLPk$’s with a magnitude between $k$ and $k+\Delta k$, independent of the direction. The “volume in $k$-space” between $k$ and $k+\Delta k$ is a spherical shell of volume \begin{equation*} 4\pi k^2\,\Delta k. \end{equation*} The number of modes is then \begin{equation} \label{Eq:III:4:40} \Delta\numModes(\omega)=\frac{V4\pi k^2\,\Delta k}{(2\pi)^3}. \end{equation} However, since we are now interested in frequencies, we should substitute $k=\omega/c$, so we get \begin{equation} \label{Eq:III:4:41} \Delta\numModes(\omega)=\frac{V4\pi\omega^2\,\Delta \omega}{(2\pi)^3c^3}. \end{equation}
There is one more complication. If we are talking about modes of an electromagnetic wave, for any given wave vector $\FLPk$ there can be either of two polarizations (at right angles to each other). Since these modes are independent, we must—for light—double the number of modes. So we have \begin{equation} \label{Eq:III:4:42} \Delta\numModes(\omega)=\frac{V\omega^2\,\Delta \omega}{\pi^2c^3} \quad(\text{for light}). \end{equation} We have shown, Eq. (4.33), that each mode (or each “state”) has on the average the energy \begin{equation*} \overline{n}\hbar\omega=\frac{\hbar\omega}{e^{\hbar\omega/\kappa T}-1}. \end{equation*} Multiplying this by the number of modes, we get the energy $\Delta E$ in the modes that lie in the interval $\Delta\omega$: \begin{equation} \label{Eq:III:4:43} \Delta E=\frac{\hbar\omega}{e^{\hbar\omega/\kappa T}-1}\, \frac{V\omega^2\,\Delta \omega}{\pi^2c^3}. \end{equation} This is the law for the frequency spectrum of blackbody radiation, which we have already found in Chapter 41 of Vol. I. The spectrum is plotted in Fig. 4–10. You see now that the answer depends on the fact that photons are Bose particles, which have a tendency to try to get all into the same state (because the amplitude for doing so is large). You will remember, it was Planck’s study of the blackbody spectrum (which was a mystery to classical physics), and his discovery of the formula in Eq. (4.43) that started the whole subject of quantum mechanics.
4–6Liquid helium
Liquid helium has at low temperatures many odd properties which we cannot unfortunately take the time to describe in detail right now, but many of them arise from the fact that a helium atom is a Bose particle. One of the things is that liquid helium flows without any viscous resistance. It is, in fact, the ideal “dry” water we have been talking about in one of the earlier chapters—provided that the velocities are low enough. The reason is the following. In order for a liquid to have viscosity, there must be internal energy losses; there must be some way for one part of the liquid to have a motion that is different from that of the rest of the liquid. This means that it must be possible to knock some of the atoms into states that are different from the states occupied by other atoms. But at sufficiently low temperatures, when the thermal motions get very small, all the atoms try to get into the same condition. So, if some of them are moving along, then all the atoms try to move together in the same state. There is a kind of rigidity to the motion, and it is hard to break the motion up into irregular patterns of turbulence, as would happen, for example, with independent particles. So in a liquid of Bose particles, there is a strong tendency for all the atoms to go into the same state—which is represented by the $\sqrt{n+1}$ factor we found earlier. (For a bottle of liquid helium $n$ is, of course, a very large number!) This cooperative motion does not happen at high temperatures, because then there is sufficient thermal energy to put the various atoms into various different higher states. But at a sufficiently low temperature there suddenly comes a moment in which all the helium atoms try to go into the same state. The helium becomes a superfluid. Incidentally, this phenomenon only appears with the isotope of helium which has atomic weight $4$. For the helium isotope of atomic weight $3$, the individual atoms are Fermi particles, and the liquid is a normal fluid. Since superfluidity occurs only with He$^4$, it is evidently a quantum mechanical effect—due to the Bose nature of the $\alpha$-particle.
4–7The exclusion principle
Fermi particles act in a completely different way. Let’s see what happens if we try to put two Fermi particles into the same state. We will go back to our original example and ask for the amplitude that two identical Fermi particles will be scattered into almost exactly the same direction. The amplitude that particle $a$ will go in direction $1$ and particle $b$ will go in direction $2$ is \begin{equation*} \braket{1}{a}\braket{2}{b}, \end{equation*} whereas the amplitude that the outgoing directions will be interchanged is \begin{equation*} \braket{2}{a}\braket{1}{b}. \end{equation*} Since we have Fermi particles, the amplitude for the process is the difference of these two amplitudes: \begin{equation} \label{Eq:III:4:44} \braket{1}{a}\braket{2}{b}-\braket{2}{a}\braket{1}{b}. \end{equation} Let’s say that by “direction $1$” we mean that the particle has not only a certain direction but also a given direction of its spin, and that “direction $2$” is almost exactly the same as direction $1$ and corresponds to the same spin direction. Then $\braket{1}{a}$ and $\braket{2}{a}$ are nearly equal. (This would not necessarily be true if the outgoing states $1$ and $2$ did not have the same spin, because there might be some reason why the amplitude would depend on the spin direction.) Now if we let directions $1$ and $2$ approach each other, the total amplitude in Eq. (4.44) becomes zero. The result for Fermi particles is much simpler than for Bose particles. It just isn’t possible at all for two Fermi particles—such as two electrons—to get into exactly the same state. You will never find two electrons in the same position with their two spins in the same direction. It is not possible for two electrons to have the same momentum and the same spin directions. If they are at the same location or with the same state of motion, the only possibility is that they must be spinning opposite to each other.
What are the consequences of this? There are a number of most remarkable effects which are a consequence of the fact that two Fermi particles cannot get into the same state. In fact, almost all the peculiarities of the material world hinge on this wonderful fact. The variety that is represented in the periodic table is basically a consequence of this one rule.
Of course, we cannot say what the world would be like if this one rule were changed, because it is just a part of the whole structure of quantum mechanics, and it is impossible to say what else would change if the rule about Fermi particles were different. Anyway, let’s just try to see what would happen if only this one rule were changed. First, we can show that every atom would be more or less the same. Let’s start with the hydrogen atom. It would not be noticeably affected. The proton of the nucleus would be surrounded by a spherically symmetric electron cloud, as shown in Fig. 4–11(a). As we have described in Chapter 2, the electron is attracted to the center, but the uncertainty principle requires that there be a balance between the concentration in space and in momentum. The balance means that there must be a certain energy and a certain spread in the electron distribution which determines the characteristic dimension of the hydrogen atom.
Now suppose that we have a nucleus with two units of charge, such as the helium nucleus. This nucleus would attract two electrons, and if they were Bose particles, they would—except for their electric repulsion—both crowd in as close as possible to the nucleus. A helium atom might look as shown in part (b) of the figure. Similarly, a lithium atom which has a triply charged nucleus would have an electron distribution like that shown in part (c) of Fig. 4–11. Every atom would look more or less the same—a little round ball with all the electrons sitting near the nucleus, nothing directional and nothing complicated.
Because electrons are Fermi particles, however, the actual situation is quite different. For the hydrogen atom the situation is essentially unchanged. The only difference is that the electron has a spin which we indicate by the little arrow in Fig. 4–12(a). In the case of a helium atom, however, we cannot put two electrons on top of each other. But wait, that is only true if their spins are the same. Two electrons can occupy the same state if their spins are opposite. So the helium atom does not look much different either. It would appear as shown in part (b) of Fig. 4–12. For lithium, however, the situation becomes quite different. Where can we put the third electron? The third electron cannot go on top of the other two because both spin directions are occupied. (You remember that for an electron or any particle with spin $1/2$ there are only two possible directions for the spin.) The third electron can’t go near the place occupied by the other two, so it must take up a special condition in a different kind of state farther away from the nucleus in part (c) of the figure. (We are speaking only in a rather rough way here, because in reality all three electrons are identical; since we cannot really distinguish which one is which, our picture is only an approximate one.)
Now we can begin to see why different atoms will have different chemical properties. Because the third electron in lithium is farther out, it is relatively more loosely bound. It is much easier to remove an electron from lithium than from helium. (Experimentally, it takes $25$ electron volts to ionize helium but only $5$ electron volts to ionize lithium.) This accounts for the valence of the lithium atom. The directional properties of the valence have to do with the pattern of the waves of the outer electron, which we will not go into at the moment. But we can already see the importance of the so-called exclusion principle—which states that no two electrons can be found in exactly the same state (including spin).
The exclusion principle is also responsible for the stability of matter on a large scale. We explained earlier that the individual atoms in matter did not collapse because of the uncertainty principle; but this does not explain why it is that two hydrogen atoms can’t be squeezed together as close as you want—why it is that all the protons don’t get close together with one big smear of electrons around them. The answer is, of course, that since no more than two electrons—with opposite spins—can be in roughly the same place, the hydrogen atoms must keep away from each other. So the stability of matter on a large scale is really a consequence of the Fermi particle nature of the electrons.
Of course, if the outer electrons on two atoms have spins in opposite directions, they can get close to each other. This is, in fact, just the way that the chemical bond comes about. It turns out that two atoms together will generally have the lowest energy if there is an electron between them. It is a kind of an electrical attraction for the two positive nuclei toward the electron in the middle. It is possible to put two electrons more or less between the two nuclei so long as their spins are opposite, and the strongest chemical binding comes about this way. There is no stronger binding, because the exclusion principle does not allow there to be more than two electrons in the space between the atoms. We expect the hydrogen molecule to look more or less as shown in Fig. 4–13.
We want to mention one more consequence of the exclusion principle. You remember that if both electrons in the helium atom are to be close to the nucleus, their spins are necessarily opposite. Now suppose that we would like to try to arrange to have both electrons with the same spin—as we might consider doing by putting on a fantastically strong magnetic field that would try to line up the spins in the same direction. But then the two electrons could not occupy the same state in space. One of them would have to take on a different geometrical position, as indicated in Fig. 4–14. The electron which is located farther from the nucleus has less binding energy. The energy of the whole atom is therefore quite a bit higher. In other words, when the two spins are opposite, there is a much stronger total attraction.
So, there is an apparent, enormous force trying to line up spins opposite to each other when two electrons are close together. If two electrons are trying to go in the same place, there is a very strong tendency for the spins to become lined opposite. This apparent force trying to orient the two spins opposite to each other is much more powerful than the tiny force between the two magnetic moments of the electrons. You remember when we were speaking of ferromagnetism there was the mystery of why the electrons in different atoms had a strong tendency to line up parallel. Although there is still no quantitative explanation, it is believed that what happens is that the electrons around the core of one atom interact through the exclusion principle with the outer electrons which have become free to wander throughout the crystal. This interaction causes the spins of the free electrons and the inner electrons to take on opposite directions. But the free electrons and the inner atomic electrons can only be opposite provided all the inner electrons have the same spin direction, as indicated in Fig. 4–15. It seems probable that it is the effect of the exclusion principle acting indirectly through the free electrons that gives rise to the strong aligning forces responsible for ferromagnetism.
We will mention one further example of the influence of the exclusion principle. We have said earlier that the nuclear forces are the same between the neutron and the proton, between the proton and the proton, and between the neutron and the neutron. Why is it then that a proton and a neutron can stick together to make a deuterium nucleus, whereas there is no nucleus with just two protons or with just two neutrons? The deuteron is, as a matter of fact, bound by an energy of about $2.2$ million electron volts, yet, there is no corresponding binding between a pair of protons to make an isotope of helium with the atomic weight $2$. Such nuclei do not exist. The combination of two protons does not make a bound state.
The answer is a result of two effects: first, the exclusion principle; and second, the fact that the nuclear forces are somewhat sensitive to the direction of spin. The force between a neutron and a proton is attractive and somewhat stronger when the spins are parallel than when they are opposite. It happens that these forces are just different enough that a deuteron can only be made if the neutron and proton have their spins parallel; when their spins are opposite, the attraction is not quite strong enough to bind them together. Since the spins of the neutron and proton are each one-half and are in the same direction, the deuteron has a spin of one. We know, however, that two protons are not allowed to sit on top of each other if their spins are parallel. If it were not for the exclusion principle, two protons would be bound, but since they cannot exist at the same place and with the same spin directions, the He$^2$ nucleus does not exist. The protons could come together with their spins opposite, but then there is not enough binding to make a stable nucleus, because the nuclear force for opposite spins is too weak to bind a pair of nucleons. The attractive force between neutrons and protons of opposite spins can be seen by scattering experiments. Similar scattering experiments with two protons with parallel spins show that there is the corresponding attraction. So it is the exclusion principle that helps explain why deuterium can exist when He$^2$ cannot.
- In (4.11) interchanging $dS_1$ and $dS_2$ gives a different event, so both surface elements should range over the whole area of the counter. In (4.13) we are treating $dS_1$ and $dS_2$ as a pair and including everything that can happen. If the integrals include again what happens when $dS_1$ and $dS_2$ are reversed, everything is counted twice. ↩