19 The Hydrogen Atom and The Periodic Table
The Hydrogen Atom and The Periodic Table

19–1Schrödinger’s equation for the hydrogen atom
The most dramatic success in the history of the quantum mechanics was the understanding of the details of the spectra of some simple atoms and the understanding of the periodicities which are found in the table of chemical elements. In this chapter we will at last bring our quantum mechanics to the point of this important achievement, specifically to an understanding of the spectrum of the hydrogen atom. We will at the same time arrive at a qualitative explanation of the mysterious properties of the chemical elements. We will do this by studying in detail the behavior of the electron in a hydrogen atom—for the first time making a detailed calculation of a distribution-in-space according to the ideas we developed in Chapter 16.
For a complete description of the hydrogen atom we should describe the motions of both the proton and the electron. It is possible to do this in quantum mechanics in a way that is analogous to the classical idea of describing the motion of each particle relative to the center of gravity, but we will not do so. We will just discuss an approximation in which we consider the proton to be very heavy, so we can think of it as fixed at the center of the atom.
We will make another approximation by forgetting that the electron has a spin and should be described by relativistic laws of mechanics. Some small corrections to our treatment will be required since we will be using the nonrelativistic Schrödinger equation and will disregard magnetic effects. Small magnetic effects occur because from the electron’s point-of-view the proton is a circulating charge which produces a magnetic field. In this field the electron will have a different energy with its spin up than with it down. The energy of the atom will be shifted a little bit from what we will calculate. We will ignore this small energy shift. Also we will imagine that the electron is just like a gyroscope moving around in space always keeping the same direction of spin. Since we will be considering a free atom in space the total angular momentum will be conserved. In our approximation we will assume that the angular momentum of the electron spin stays constant, so all the rest of the angular momentum of the atom—what is usually called “orbital” angular momentum—will also be conserved. To an excellent approximation the electron moves in the hydrogen atom like a particle without spin—the angular momentum of the motion is a constant.
With these approximations the amplitude to find the electron at different places in space can be represented by a function of position in space and time. We let $\psi(x,y,z,t)$ be the amplitude to find the electron somewhere at the time $t$. According to the quantum mechanics the rate of change of this amplitude with time is given by the Hamiltonian operator working on the same function. From Chapter 16, \begin{equation} \label{Eq:III:19:1} i\hbar\,\ddp{\psi}{t}=\Hcalop\psi, \end{equation} with \begin{equation} \label{Eq:III:19:2} \Hcalop=-\frac{\hbar^2}{2m}\,\nabla^2+V(\FLPr). \end{equation} Here, $m$ is the electron mass, and $V(\FLPr)$ is the potential energy of the electron in the electrostatic field of the proton. Taking $V=0$ at large distances from the proton we can write1 \begin{equation*} V=-\frac{e^2}{r}. \end{equation*} The wave function $\psi$ must then satisfy the equation \begin{equation} \label{Eq:III:19:3} i\hbar\,\ddp{\psi}{t}=-\frac{\hbar^2}{2m}\,\nabla^2\psi -\frac{e^2}{r}\,\psi. \end{equation}
We want to look for definite energy states, so we try to find solutions which have the form \begin{equation} \label{Eq:III:19:4} \psi(\FLPr,t)=e^{-(i/\hbar)Et}\psi(\FLPr). \end{equation} The function $\psi(\FLPr)$ must then be a solution of \begin{equation} \label{Eq:III:19:5} -\frac{\hbar^2}{2m}\,\nabla^2\psi= \biggl(E+\frac{e^2}{r}\biggr)\psi, \end{equation} where $E$ is some constant—the energy of the atom.
Since the potential energy term depends only on the radius, it turns out to be much more convenient to solve this equation in polar coordinates rather than rectangular coordinates. The Laplacian is defined in rectangular coordinates by \begin{equation*} \nabla^2=\frac{\partial^2}{\partial x^2}+ \frac{\partial^2}{\partial y^2}+ \frac{\partial^2}{\partial z^2}. \end{equation*} We want to use instead the coordinates $r$, $\theta$, $\phi$ shown in Fig. 19–1. These coordinates are related to $x$, $y$, $z$ by \begin{equation*} x=r\sin\theta\cos\phi;\quad y=r\sin\theta\sin\phi;\quad z=r\cos\theta. \end{equation*} It’s a rather tedious mess to work through the algebra, but you can eventually show that for any function $f(\FLPr)=f(r,\theta,\phi)$, \begin{equation} \label{Eq:III:19:6} \nabla^2f(r,\theta,\phi)=\frac{1}{r}\,\frac{\partial^2}{\partial r^2}\, (rf)+\frac{1}{r^2}\biggl\{ \frac{1}{\sin\theta}\,\ddp{}{\theta}\biggl( \sin\theta\,\ddp{f}{\theta}\biggr)+\frac{1}{\sin^2\theta}\, \frac{\partial^2f}{\partial\phi^2}\biggr\}. \end{equation} So in terms of the polar coordinates, the equation which is to be satisfied by $\psi(r,\theta,\phi)$ is \begin{equation} \label{Eq:III:19:7} \frac{1}{r}\,\frac{\partial^2}{\partial r^2}\, (r\psi)+\frac{1}{r^2}\biggl\{ \frac{1}{\sin\theta}\,\ddp{}{\theta}\biggl( \sin\theta\,\ddp{\psi}{\theta}\biggr)+\frac{1}{\sin^2\theta}\, \frac{\partial^2\psi}{\partial \phi^2}\biggr\}= -\frac{2m}{\hbar^2}\biggl(E+\frac{e^2}{r}\biggr)\psi. \end{equation}
19–2Spherically symmetric solutions
Let’s first try to find some very simple function that satisfies the horrible equation in (19.7). Although the wave function $\psi$ will, in general, depend on the angles $\theta$ and $\phi$ as well as on the radius $r$, we can see whether there might be a special situation in which $\psi$ does not depend on the angles. For a wave function that doesn’t depend on the angles, none of the amplitudes will change in any way if you rotate the coordinate system. That means that all of the components of the angular momentum are zero. Such a $\psi$ must correspond to a state whose total angular momentum is zero. (Actually, it is only the orbital angular momentum which is zero because we still have the spin of the electron, but we are ignoring that part.) A state with zero orbital angular momentum is called by a special name. It is called an “$s$-state”—you can remember “$s$ for spherically symmetric.”2
Now if $\psi$ is not going to depend on $\theta$ and $\phi$ then the entire Laplacian contains only the first term and Eq. (19.7) becomes much simpler: \begin{equation} \label{Eq:III:19:8} \frac{1}{r}\,\frac{d^2}{dr^2}\,(r\psi)= -\frac{2m}{\hbar^2}\biggl(E+\frac{e^2}{r}\biggr)\psi. \end{equation} Before you start to work on solving an equation like this, it’s a good idea to get rid of all excess constants like $e^2$, $m$, and $\hbar$, by making some scale changes. Then the algebra will be easier. If we make the following substitutions: \begin{equation} \label{Eq:III:19:9} r=\frac{\hbar^2}{me^2}\,\rho, \end{equation} and \begin{equation} \label{Eq:III:19:10} E=\frac{me^4}{2\hbar^2}\,\epsilon, \end{equation} then Eq. (19.8) becomes (after multiplying through by $\rho$) \begin{equation} \label{Eq:III:19:11} \frac{d^2(\rho\psi)}{d\rho^2}= -\biggl(\epsilon+\frac{2}{\rho}\biggr)\rho\psi. \end{equation} These scale changes mean that we are measuring the distance $r$ and energy $E$ as multiples of “natural” atomic units. That is, $\rho=r/r_B$, where $r_B=\hbar^2/me^2$, is called the “Bohr radius” and is about $0.528$ angstroms. Similarly, $\epsilon=E/E_R$, with $E_R=me^4/2\hbar^2$. This energy is called the “Rydberg” and is about $13.6$ electron volts.
Since the product $\rho\psi$ appears on both sides, it is convenient to work with it rather than with $\psi$ itself. Letting \begin{equation} \label{Eq:III:19:12} \rho\psi=f, \end{equation} we have the more simple-looking equation \begin{equation} \label{Eq:III:19:13} \frac{d^2f}{d\rho^2}=-\biggl(\epsilon+\frac{2}{\rho}\biggr)f. \end{equation}
Now we have to find some function $f$ which satisfies Eq. (19.13)—in other words, we just have to solve a differential equation. Unfortunately, there is no very useful, general method for solving any given differential equation. You just have to fiddle around. Our equation is not easy, but people have found that it can be solved by the following procedure. First, you replace $f$, which is some function of $\rho$, by a product of two functions \begin{equation} \label{Eq:III:19:14} f(\rho)=e^{-\alpha\rho}g(\rho). \end{equation} This just means that you are factoring $e^{-\alpha\rho}$ out of $f(\rho)$. You can certainly do that for any $f(\rho)$ at all. This just shifts our problem to finding the right function $g(\rho)$.
Sticking (19.14) into (19.13), we get the following equation for $g$: \begin{equation} \label{Eq:III:19:15} \frac{d^2g}{d\rho^2}-2\alpha\,\ddt{g}{\rho}+\biggl( \frac{2}{\rho}+\epsilon+\alpha^2\biggr)g=0. \end{equation} Since we are free to choose $\alpha$, let’s make \begin{equation} \label{Eq:III:19:16} \alpha^2=-\epsilon, \end{equation} and get \begin{equation} \label{Eq:III:19:17} \frac{d^2g}{d\rho^2}-2\alpha\,\ddt{g}{\rho}+ \frac{2}{\rho}\,g=0. \end{equation}
You may think we are no better off than we were at Eq. (19.13), but the happy thing about our new equation is that it can be solved easily in terms of a power series in $\rho$. (It is possible, in principle, to solve (19.13) that way too, but it is much harder.) We are saying that Eq. (19.17) can be satisfied by some $g(\rho)$ which can be written as a series, \begin{equation} \label{Eq:III:19:18} g(\rho)=\sum_{k=1}^\infty a_k\rho^k, \end{equation} in which the $a_k$ are constant coefficients. Now all we have to do is find a suitable infinite set of coefficients! Let’s check to see that such a solution will work. The first derivative of this $g(\rho)$ is \begin{equation*} \ddt{g}{\rho}=\sum_{k=1}^\infty a_kk\rho^{k-1}, \end{equation*} and the second derivative is \begin{equation*} \frac{d^2g}{d\rho^2}=\sum_{k=1}^\infty a_kk(k-1)\rho^{k-2}. \end{equation*} Using these expressions in (19.17) we have \begin{equation} \label{Eq:III:19:19} \sum_{k=1}^\infty \!k(k\!-\!1)a_k\rho^{k\!-\!2}\!-\!\! \sum_{k=1}^\infty \!2\alpha ka_k\rho^{k\!-\!1}\!+\!\! \sum_{k=1}^\infty \!2a_k\rho^{k\!-\!1}\!= 0. \end{equation} It’s not obvious that we have succeeded; but we forge onward. It will all look better if we replace the first sum by an equivalent. Since the first term of the sum is zero, we can replace each $k$ by $k+1$ without changing anything in the infinite series; with this change the first sum can equally well be written as \begin{equation*} \sum_{k=1}^\infty(k+1)ka_{k+1}\rho^{k-1}. \end{equation*} Now we can put all the sums together to get \begin{equation} \label{Eq:III:19:20} \sum_{k=1}^\infty[(k+1)ka_{k+1}-2\alpha ka_k+2a_k]\rho^{k-1}=0. \end{equation}
This power series must vanish for all possible values of $\rho$. It can do that only if the coefficient of each power of $\rho$ is separately zero. We will have a solution for the hydrogen atom if we can find a set $a_k$ for which \begin{equation} \label{Eq:III:19:21} (k+1)ka_{k+1}-2(\alpha k-1)a_k=0 \end{equation} for all $k\geq1$. That is certainly easy to arrange. Pick any $a_1$ you like. Then generate all of the other coefficients from \begin{equation} \label{Eq:III:19:22} a_{k+1}=\frac{2(\alpha k-1)}{k(k+1)}\,a_k. \end{equation} With this you will get $a_2$, $a_3$, $a_4$, and so on, and each pair will certainly satisfy (19.21). We get a series for $g(\rho)$ which satisfies (19.17). With it we can make a $\psi$, that satisfies Schrödinger’s equation. Notice that the solutions depend on the assumed energy (through $\alpha$), but for each value of $\epsilon$, there is a corresponding series.
We have a solution, but what does it represent physically? We can get an idea by seeing what happens far from the proton—for large values of $\rho$. Out there, the high-order terms of the series are the most important, so we should look at what happens for large $k$. When $k\gg1$, Eq. (19.22) is approximately the same as \begin{equation*} a_{k+1}=\frac{2\alpha}{k}\,a_k, \end{equation*} which means that \begin{equation} \label{Eq:III:19:23} a_{k+1}\approx\frac{(2\alpha)^k}{k!}. \end{equation} But these are just the coefficients of the series for $e^{+2\alpha\rho}$. The function of $g$ is a rapidly increasing exponential. Even coupled with $e^{-\alpha\rho}$ to produce $f(\rho)$—see Eq. (19.14)—it still gives a solution for $f(\rho)$ which goes like $e^{\alpha\rho}$ for large $\rho$. We have found a mathematical solution but not a physical one. It represents a situation in which the electron is least likely to be near the proton! It is always more likely to be found at a very large radius $\rho$. A wave function for a bound electron must go to zero for large $\rho$.
We have to think whether there is some way to beat the game, and there is. Observe! If it just happened by luck that $\alpha$ were equal to $1/n$, where $n$ is any positive integer, then Eq. (19.22) would make $a_{n+1}=0$. All higher terms would also be zero. We wouldn’t have an infinite series but a finite polynomial. Any polynomial increases more slowly than $e^{\alpha\rho}$, so the term $e^{-\alpha\rho}$ will eventually beat it down, and the function $f$ will go to zero for large $\rho$. The only bound-state solutions are those for which $\alpha=1/n$, with $n=1$, $2$, $3$, $4$, and so on.
Looking back to Eq. (19.16), we see that the bound-state solutions to the spherically symmetric wave equation can exist only when \begin{equation*} -\epsilon=1,\,\frac{1}{4},\,\frac{1}{9},\,\frac{1}{16},\dotsc, \frac{1}{n^2},\dotsc \end{equation*} The allowed energies are just these fractions times the Rydberg, $E_R=me^4/2\hbar^2$, or the energy of the $n$th energy level is \begin{equation} \label{Eq:III:19:24} E_n=-E_R\,\frac{1}{n^2}. \end{equation} There is, incidentally, nothing mysterious about negative numbers for the energy. The energies are negative because when we chose to write $V=-e^2/r$, we picked our zero point as the energy of an electron located far from the proton. When it is close to the proton, its energy is less, so somewhat below zero. The energy is lowest (most negative) for $n=1$, and increases toward zero with increasing $n$.
Before the discovery of quantum mechanics, it was known from experimental studies of the spectrum of hydrogen that the energy levels could be described by Eq. (19.24), where $E_R$ was found from the observations to be about $13.6$ electron volts. Bohr then devised a model which gave the same equation and predicted that $E_R$ should be $me^4/2\hbar^2$. But it was the first great success of the Schrödinger theory that it could reproduce this result from a basic equation of motion for the electron.
Now that we have solved our first atom, let’s look at the nature of the solution we got. Pulling all the pieces together, each solution looks like this: \begin{equation} \label{Eq:III:19:25} \psi_n=\frac{f_n(\rho)}{\rho}=\frac{e^{-\rho/n}}{\rho}\,g_n(\rho), \end{equation} where \begin{equation} \label{Eq:III:19:26} g_n(\rho)=\sum_{k=1}^na_k\rho^k \end{equation} and \begin{equation} \label{Eq:III:19:27} a_{k+1}=\frac{2(k/n-1)}{k(k+1)}\,a_k. \end{equation} So long as we are mainly interested in the relative probabilities of finding the electron at various places we can pick any number we wish for $a_1$. We may as well set $a_1=1$. (People often choose $a_1$ so that the wave function is “normalized,” that is, so that the integrated probability of finding the electron anywhere in the atom is equal to $1$. We have no need to do that just now.)
For the lowest energy state, $n=1$, and \begin{equation} \label{Eq:III:19:28} \psi_1(\rho)=e^{-\rho}. \end{equation} For a hydrogen atom in its ground (lowest-energy) state, the amplitude to find the electron at any point drops off exponentially with the distance from the proton. It is most likely to be found right at the proton, and the characteristic spreading distance is about one unit in $\rho$, or about one Bohr radius, $r_B$.
Putting $n=2$ gives the next higher level. The wave function for this state will have two terms. It is \begin{equation} \label{Eq:III:19:29} \psi_2(\rho)=\biggl(1-\frac{\rho}{2}\biggr)e^{-\rho/2}. \end{equation} The wave function for the next level is \begin{equation} \label{Eq:III:19:30} \psi_3(\rho)=\biggl(1-\frac{2\rho}{3}+\frac{2}{27}\,\rho^2\biggr) e^{-\rho/3}. \end{equation} The wave functions for these first three levels are plotted in Fig. 19–2. You can see the general trend. All of the wave functions approach zero rapidly for large $\rho$ after oscillating a few times. In fact, the number of “bumps” is just equal to $n$—or, if you prefer, the number of zero-crossings of $\psi_n$ is $n-1$.
2019.12.2: 'the number of “bumps” is just equal to n' 증명
$\psi_n=\frac1{\rho}e^{-\frac{\rho}n}g_n, \,여기서
\, g_n(\rho)=\sum_{k=1}^n a_k\rho^k, \, a_1=1, \, a_{k+1}=\frac{2(\frac{k}{n} -1)}{k(k+1)}a_k, \\
\frac{d^2g}{d\rho^2} - \text{constant}\times \frac{dg}{d\rho}+\frac{2}{\rho}g=0 <=> g\prime\prime- \text{constant}\times g\prime+\frac{2}{\rho}g=0(g\, 인덱스\, n\, 생략)$
위식에서 $g$가 0 이외에 $(n-1)$개의 근을 갖는다는 것을 증명하는 것. 만만하게 보고 달려 들었는데, 1달여간을 해맸다, 함수 자체를 이리저리 분석하고 그래프도 찍어보고 등등.
그러다 아주 재미있는 증명 발견! 핵심은 $g$ 에 대한 마지막 미분방정식에 있다.
$\alpha$를 $g'(\alpha)=0$를 만족하는 해라고 하면(* $k$ 홀수/짝수 => $a_k$ 양수/음수이고 $\rho$ < 0인 경우, $g$ <0 이니, $\alpha$ >0일 때만 따지면 된다)
(1) $g''(\alpha)-\text{constant}\times g'(\alpha)+\frac{2}{\rho}g(\alpha)=0$ 으로부터',
$g''(\alpha)$ 는 $g(\alpha)$와 부호가 반대라는 것.
이것을 기하학적으로 풀이하면, $\alpha$ 좌우로 $x$축을 만날 때까지 증가하거나 감소하여야 한다는 것, 즉 아래 왼쪽 그림과 같은 그래프는 불가능하며, 오른쪽 그림과 같이 항상 x 축을 만나야 한다는 것.
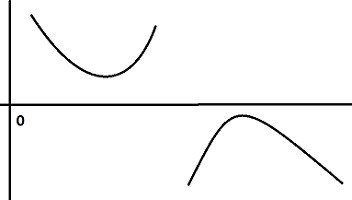

(2) $g''(\alpha)$ 값이 0이 될 수 없다. 아닌 경우, 마지막 방정식의 선형적 성질에 의하여 모든 derivative 값이 0이 되고 이는 nth derivative 값이 0이 아니라는 사실과 배치.
$g$ 그래프는 아래와 같은 형성 과정을 거칠 수 없다는 것.
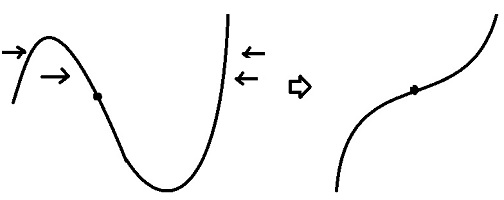
=> (1), (2)로 부터 $g$는 0을 포함하여 n개의 근을 갖는다.
19–3States with an angular dependence
In the states described by the $\psi_n(r)$ we have found that the probability amplitude for finding the electron is spherically symmetric—depending only on $r$, the distance for the proton. Such states have zero orbital angular momentum. We should now inquire about states which may have some angular dependences.
We could, if we wished, just investigate the strictly mathematical problem of finding the functions of $r$, $\theta$, and $\phi$ which satisfy the differential equation (19.7)—putting in the additional physical conditions that the only acceptable functions are ones which go to zero for large $r$. You will find this done in many books. We are going to take a short cut by using the knowledge we already have about how amplitudes depend on angles in space.
The hydrogen atom in any particular state is a particle with a certain “spin” $j$—the quantum number of the total angular momentum. Part of this spin comes from the electron’s intrinsic spin, and part from the electron’s motion. Since each of these two components acts independently (to an excellent approximation) we will again ignore the spin part and think only about the “orbital” angular momentum. This orbital motion behaves, however, just like a spin. For example, if the orbital quantum number is $l$, the $z$-component of angular momentum can be $l$, $l-1$, $l-2$, …, $-l$. (We are, as usual, measuring in units of $\hbar$.) Also, all the rotation matrices and other properties we have worked out still apply. (From now on we will really ignore the electron’s spin; when we speak of “angular momentum” we will mean only the orbital part.)
Since the potential $V$ in which the electron moves depends only on $r$ and not on $\theta$ or $\phi$, the Hamiltonian is symmetric under all rotations. It follows that the angular momentum and all its components are conserved. (This is true for motion in any “central field”—one which depends only on $r$—so is not a special feature of the Coulomb $e^2/r$ potential.)
Now let’s think of some possible state of the electron; its internal angular structure will be characterized by the quantum number $l$. Depending on the “orientation” of the total angular momentum with respect to the $z$-axis, the $z$-component of angular momentum will be $m$, which is one of the $2l+1$ possibilities between $+l$ and $-l$. Let’s say $m=1$. With what amplitude will the electron be found on the $z$-axis at some distance $r$? Zero. An electron on the $z$-axis cannot have any orbital angular momentum around that axis. Alright, suppose $m$ is zero, then there can be some nonzero amplitude to find the electron at each distance from the proton. We’ll call this amplitude $F_l(r)$. It is the amplitude to find the electron at the distance $r$ up along the $z$-axis, when the atom is in the state $\ket{l,0}$, by which we mean orbital spin $l$ and $z$-component $m=0$.
If we know $F_l(r)$ everything is known. For any state $\ket{l,m}$, we know the amplitude $\psi_{l,m}(\FLPr)$ to find the electron anywhere in the atom. How? Watch. Suppose we have the atom in the state $\ket{l,m}$, what is the amplitude to find the electron at the angle $\theta,\phi$ and the distance $r$ from the origin? Put a new $z$-axis, say $z'$, at that angle (see Fig. 19–3), and ask what is the amplitude that the electron will be at the distance $r$ along the new axis $z'$? We know that it cannot be found along $z'$ unless its $z'$-component of angular momentum, say $m'$, is zero. When $m'$ is zero, however, the amplitude to find the electron along $z'$ is $F_l(r)$. Therefore, the result is the product of two factors. The first is the amplitude that an atom in the state $\ket{l,m}$ along the $z$-axis will be in the state $\ket{l,m'=0}$ with respect to the $z'$-axis. Multiply that amplitude by $F_l(r)$ and you have the amplitude $\psi_{l,m}(\FLPr)$ to find the electron at $(r,\theta,\phi)$ with respect to the original axes.
Let’s write it out. We have worked out earlier the transformation matrices for rotations. To go from the frame $x,y,z$ to the frame $x',y',z'$ of Fig. 19–3, we can rotate first around the $z$-axis by the angle $\phi$, and then rotate about the new $y$-axis ($y'$) by the angle $\theta$. This combined rotation is the product \begin{equation*} R_y(\theta)R_z(\phi). \end{equation*} The amplitude to find the state $l,m'=0$ after the rotation is \begin{equation} \label{Eq:III:19:31} \bracket{l,0}{R_y(\theta)R_z(\phi)}{l,m}. \end{equation} Our result, then, is \begin{equation} \label{Eq:III:19:32} \psi_{l,m}(\FLPr)=\bracket{l,0}{R_y(\theta)R_z(\phi)}{l,m}F_l(r). \end{equation}
The orbital motion can have only integral values of $l$. (If the electron can be found anywhere at $r\neq0$, there is some amplitude to have $m=0$ in that direction. And $m=0$ states exist only for integral spins.) The rotation matrices for $l=1$ are given in Table 17–2. For larger $l$ you can use the general formulas we worked out in Chapter 18. The matrices for $R_z(\phi)$ and $R_y(\theta)$ appear separately, but you know how to combine them. For the general case you would start with the state $\ket{l,m}$ and operate with $R_z(\phi)$ to get the new state $R_z(\phi)\,\ket{l,m}$ (which is just $e^{im\phi}\,\ket{l,m}$). Then you operate on this state with $R_y(\theta)$ to get the state $R_y(\theta)R_z(\phi)\,\ket{l,m}$. Multiplying by $\bra{l,0}$ gives the matrix element (19.31).
The matrix elements of the rotation operation are functions of $\theta$ and $\phi$. The particular functions which appear in (19.31) also show up in many kinds of problems which involve waves in spherical geometries and so has been given a special name. Not everyone uses the same convention; but one of the most common ones is \begin{equation} \label{Eq:III:19:33} \bracket{l,0}{R_y(\theta)R_z(\phi)}{l,m}\equiv a\,Y_{l,m}(\theta,\phi). \end{equation} The functions $Y_{l,m}(\theta,\phi)$ are called the spherical harmonics, and $a$ is just a numerical factor which depends on the definition chosen for $Y_{l,m}$. For the usual definition, \begin{equation} \label{Eq:III:19:34} a=\sqrt{\frac{4\pi}{2l+1}}. \end{equation} With this notation, the hydrogen wave functions can be written \begin{equation} \label{Eq:III:19:35} \psi_{l,m}(\FLPr)=a\,Y_{l,m}(\theta,\phi)F_l(r). \end{equation}
The angle functions $Y_{l,m}(\theta,\phi)$ are important not only in many quantum-mechanical problems, but also in many areas of classical physics in which the $\nabla^2$ operator appears, such as electromagnetism. As another example of their use in quantum mechanics, consider the disintegration of an excited state of Ne$^{20}$ (such as we discussed in the last chapter) which decays by emitting an $\alpha$-particle and going into O$^{16}$: \begin{equation*} \text{Ne}^{20*}\to\text{O}^{16}+\text{He}^4. \end{equation*} Suppose that the excited state has some spin $l$ (necessarily an integer) and that the $z$-component of angular momentum is $m$. We might now ask the following: given $l$ and $m$, what is the amplitude that we will find the $\alpha$-particle going off in a direction which makes the angle $\theta$ with respect to the $z$-axis and the angle $\phi$ with respect to the $xz$-plane—as shown in Fig. 19–4.
To solve this problem we make, first, the following observation. A decay in which the $\alpha$-particle goes straight up along $z$ must come from a state with $m=0$. This is so because both O$^{16}$ and the $\alpha$-particle have spin zero, and because their motion cannot have any angular momentum about the $z$-axis. Let’s call this amplitude $a$ (per unit solid angle). Then, to find the amplitude for a decay at the arbitrary angle of Fig. 19–4, all we need to know is what amplitude the given initial state has zero angular momentum about the decay direction. The amplitude for the decay at $\theta$ and $\phi$ is then $a$ times the amplitude that a state $\ket{l,m}$ with respect to the $z$-axis will be in the state $\ket{l,0}$ with respect to $z'$—the decay direction. This latter amplitude is just what we have written in (19.31). The probability to see the $\alpha$-particle at $\theta,\phi$ is \begin{equation*} P(\theta,\phi)=a^2\abs{\bracket{l,0}{R_y(\theta)R_z(\phi)}{l,m}}^2. \end{equation*}
As an example, consider an initial state with $l=1$ and various values of $m$. From Table 17–2 we know the necessary amplitudes. They are \begin{equation} \begin{aligned} \bracket{1,0}{R_y(\theta)R_z(\phi)}{1,+1}&= -\frac{1}{\sqrt{2}}\sin\theta e^{i\phi},\\[1ex] \bracket{1,0}{R_y(\theta)R_z(\phi)}{1,0}&=\cos\theta,\\[1ex] \bracket{1,0}{R_y(\theta)R_z(\phi)}{1,-1}&= \frac{1}{\sqrt{2}}\sin\theta e^{-i\phi}. \end{aligned} \label{Eq:III:19:36} \end{equation} These are the three possible angular distribution amplitudes—depending on the $m$-value of the initial nucleus.
Amplitudes such as the ones in (19.36) appear so often and are sufficiently important that they are given several names. If the angular distribution amplitude is proportional to any one of the three functions or any linear combination of them, we say, “The system has an orbital angular momentum of one.” Or we may say, “The Ne$^{20*}$ emits a $p$-wave $\alpha$-particle.” Or we say, “The $\alpha$-particle is emitted in an $l=1$ state.” Because there are so many ways of saying the same thing it is useful to have a dictionary. If you are going to understand what other physicists are talking about, you will just have to memorize the language. In Table 19–1 we give a dictionary of orbital angular momentum.
($l=j=$ an integer)
| Orbital angular momentum, $l$ | $z$-component,$m$ | Angular dependence of amplitudes | Name | Number of States | Orbital parity |
| $0$ | $0$ | $1$ | $s$ | $1$ | $+$ |
| $1$ | $\displaystyle\begin{equation*} \left\{ \begin{aligned} +&1\\\\ &0\\\\ -&1 \end{aligned} \right. \end{equation*}$ | $\displaystyle\begin{equation*} \left. \begin{aligned} -\dfrac{1}{\sqrt{2}}&\sin\theta e^{i\phi}\\ &\cos\theta\\ \dfrac{1}{\sqrt{2}}&\sin\theta e^{-i\phi} \end{aligned} \right\} \end{equation*}$ | $p$ | $3$ | $-$ |
| $2$ | $\displaystyle\begin{equation*} \left\{ \begin{aligned} \\ +&2\\\\ +&1\\\\ &0\\\\ -&1\\\\ -&2\\ \\ \end{aligned} \right. \end{equation*}$ | $\displaystyle\begin{equation*} \left. \begin{aligned} &\dfrac{\sqrt{6}}{4}\sin^2\theta e^{2i\phi}\\[1ex] -&\dfrac{\sqrt{6}}{2}\sin\theta\cos\theta e^{i\phi}\\[1ex] &\tfrac{1}{2}(3\cos^2\theta-1)\\[1ex] &\dfrac{\sqrt{6}}{2}\sin\theta\cos\theta e^{-i\phi}\\[1ex] &\dfrac{\sqrt{6}}{4}\sin^2\theta e^{-2i\phi}\\ \end{aligned} \right\} \end{equation*}$ | $d$ | $5$ | $+$ |
| $3\\[2ex]4\\[2ex]5$ | $\displaystyle\begin{equation*} \left\} \begin{aligned} \\ \quad\quad&\phantom{3}\quad\\[1ex] \quad\quad&\phantom{4}\quad\\[1ex] \quad\quad&\phantom{5}\quad\\ \end{aligned} \right\{ \end{equation*}$ | $\displaystyle\begin{equation*} \left. \begin{aligned} &\bracket{l,0}{R_y(\theta)R_z(\phi)}{l,m}\\[1ex] &\propto Y_{l,m}(\theta,\phi)\\[1ex] &\propto P_l^m(\cos\theta)e^{im\phi}\\[1ex] \end{aligned} \right\} \end{equation*}$ | $f\\[2ex]g\\[2ex]h$ | $2l+1$ | $(-1)^l$ |
| $\vdots$ | $\vdots$ |
If the orbital angular momentum is zero, then there is no change when you rotate the coordinate system and there is no variation with angle—the “dependence” on angle is as a constant, say $1$. This is also called an “$s$-state”, and there is only one such state—as far as angular dependence is concerned. If the orbital angular momentum is $1$, then the amplitude of the angular variation may be any one of the three functions given—depending on the value of $m$—or it may be a linear combination. These are called “$p$-states,” and there are three of them. If the orbital angular momentum is $2$ then there are the five functions shown. Any linear combination is called an “$l=2$,” or a “$d$-wave” amplitude. Now you can immediately guess what the next letter is—what should come after $s$, $p$, $d$? Well, of course, $f$, $g$, $h$, and so on down the alphabet! The letters don’t mean anything. (They did once mean something—they meant “sharp” lines, “principal” lines, “diffuse” lines and “fundamental” lines of the optical spectra of atoms. But those were in the days when people did not know where the lines came from. After $f$ there were no special names, so we now just continue with $g$, $h$, and so on.)
The angular functions in the table go by several names—and are sometimes defined with slightly different conventions about the numerical factors that appear out in front. Sometimes they are called “spherical harmonics,” and written as $Y_{l,m}(\theta,\phi)$. Sometimes they are written $P_l^m(\cos\theta)e^{im\phi}$, and if $m=0$, simply as $P_l(\cos\theta)$. The functions $P_l(\cos\theta)$ are called the “Legendre polynomials” in $\cos\theta$, and the functions $P_l^m(\cos\theta)$ are called the “associated Legendre functions.” You will find tables of these functions in many books.
Notice, incidentally, that all the functions for a given $l$ have the property that they have the same parity—for odd $l$ they change sign under an inversion and for even $l$ they don’t change. So we can write that the parity of a state of orbital angular momentum $l$ is $(-1)^l$.
As we have seen, these angular distributions may refer to a nuclear disintegration or some other process, or to the distribution of the amplitude to find an electron at some place in the hydrogen atom. For instance, if an electron is in a $p$-state ($l=1$) the amplitude to find it can depend on the angle in many possible ways—but all are linear combinations of the three functions for $l=1$ in Table 19–1. Let’s take the case $\cos\theta$. That’s interesting. That means that the amplitude is positive, say, in the upper part ($\theta < \pi/2$), is negative in the lower part ($\theta > \pi/2$), and is zero when $\theta$ is $90^\circ$. Squaring this amplitude we see that the probability of finding the electron varies with $\theta$ as shown in Fig. 19–5—and is independent of $\phi$. This angular distribution is responsible for the fact that in molecular binding the attraction of an electron in an $l=1$ state for another atom depends on direction—it is the origin of the directed valences of chemical attraction.
19–4The general solution for hydrogen
In Eq. (19.35) we have written the wave functions for the hydrogen atom as \begin{equation} \label{Eq:III:19:37} \psi_{l,m}(\FLPr)=a\,Y_{l,m}(\theta,\phi)F_l(r). \end{equation} These wave functions must be solutions of the differential equation (19.7). Let’s see what that means. Put (19.37) into (19.7); you get \begin{align} \frac{Y_{l,m}}{r}\,\frac{\partial^2}{\partial r^2}\, (rF_l)+\frac{F_l}{r^2\sin\theta}\,\ddp{}{\theta}&\biggl( \sin\theta\,\ddp{Y_{l,m}}{\theta}\biggr)+ \frac{F_l}{r^2\sin^2\theta}\,\frac{\partial^2Y_{l,m}} {\partial\phi^2}\notag\\[1ex] \label{Eq:III:19:38} &=\;-\frac{2m}{\hbar^2}\biggl(E+\frac{e^2}{r}\biggr) Y_{l,m}F_l. \end{align} Now multiply through by $r^2/F_l$ and rearrange terms. The result is \begin{align} \frac{1}{\sin\theta}\,\ddp{}{\theta}&\biggl( \sin\theta\,\ddp{Y_{l,m}}{\theta}\biggr)+ \frac{1}{\sin^2\theta}\,\frac{\partial^2Y_{l,m}} {\partial\phi^2}\notag\\[1ex] \label{Eq:III:19:39} &=\;-\biggl[ \frac{r^2}{F_l}\biggl\{ \frac{1}{r}\,\frac{d^2}{dr^2}\,(rF_l)+\frac{2m}{\hbar^2} \biggl(E+\frac{e^2}{r}\biggr)F_l\biggr\}\biggr]Y_{l,m}. \end{align} The left-hand side of this equation depends on $\theta$ and $\phi$, but not on $r$. No matter what value we choose for $r$, the left side doesn’t change. This must also be true for the right-hand side. Although the quantity in the square brackets has $r$’s all over the place, the whole quantity cannot depend on $r$, otherwise we wouldn’t have an equation good for all $r$. As you can see, the bracket also does not depend on $\theta$ or $\phi$. It must be some constant. Its value may well depend on the $l$-value of the state we are studying, since the function $F_l$ must be the one appropriate to that state; we’ll call the constant $K_l$. Equation (19.39) is therefore equivalent to two equations: \begin{gather} \label{Eq:III:19:40} \frac{1}{\sin\theta}\,\ddp{}{\theta}\biggl( \sin\theta\,\ddp{Y_{l,m}}{\theta}\biggr)+ \frac{1}{\sin^2\theta}\,\frac{\partial^2Y_{l,m}} {\partial\phi^2}=-K_lY_{l,m},\\ \notag\\[2pt] \label{Eq:III:19:41} \frac{1}{r}\,\frac{d^2}{dr^2}\,(rF_l)+ \frac{2m}{\hbar^2}\biggl(E+\frac{e^2}{r}\biggr)F_l= K_l\,\frac{F_l}{r^2}. \end{gather}
Now look at what we’ve done. For any state described by $l$ and $m$, we know the functions $Y_{l,m}$; we can use Eq. (19.40) to determine the constant $K_l$. Putting $K_l$ into Eq. (19.41) we have a differential equation for the function $F_l(r)$. If we can solve that equation for $F_l(r)$, we have all of the pieces to put into (19.37) to give $\psi(\FLPr)$.
What is $K_l$? First, notice that it must be the same for all $m$ (which go with a particular $l$), so we can pick any $m$ we want for $Y_{l,m}$ and plug it into (19.40) to solve for $K_l$. Perhaps the easiest one to use is $Y_{l,l}$. From Eq. (18.24), \begin{equation} \label{Eq:III:19:42} R_z(\phi)\,\ket{l,l}=e^{il\phi}\,\ket{l,l}. \end{equation} The matrix element for $R_y(\theta)$ is also quite simple: \begin{equation} \label{Eq:III:19:43} \bracket{l,0}{R_y(\theta)}{l,l}=b\,(\sin\theta)^l, \end{equation} where $b$ is some number.3 Combining the two, we obtain \begin{equation} \label{Eq:III:19:44} Y_{l,l}\propto e^{il\phi}\sin^l\theta. \end{equation} Putting this function into (19.40) gives \begin{equation} \label{Eq:III:19:45} K_l=l(l+1). \end{equation}
Now that we have determined $K_l$, Eq. (19.41) tells us about the radial function $F_l(r)$. It is, of course, just the Schrödinger equation with the angular part replaced by its equivalent $K_lF_l/r^2$. Let’s rewrite (19.41) in the form we had in Eq. (19.8), as follows: \begin{equation} \label{Eq:III:19:46} \frac{1}{r}\frac{d^2}{dr^2}(rF_l)= -\frac{2m}{\hbar^2}\biggl\{\! E\!+\!\frac{e^2}{r}\!-\!\frac{l(l\!+\!1)\hbar^2}{2mr^2} \!\biggr\}F_l. \end{equation} A mysterious term has been added to the potential energy. Although we got this term by some mathematical shenanigan, it has a simple physical origin. We can give you an idea about where it comes from in terms of a semi-classical argument. Then perhaps you will not find it quite so mysterious.
Think of a classical particle moving around some center of force. The total energy is conserved and is the sum of the potential and kinetic energies \begin{equation*} U = V(r) + \tfrac{1}{2}mv^2 = \text{constant}. \end{equation*} In general, $v$ can be resolved into a radial component $v_r$ and a tangential component $r\dot{\theta}$; then \begin{equation*} v^2=v_r^2+(r\dot{\theta})^2. \end{equation*} Now the angular momentum $mr^2\dot{\theta}$ is also conserved; say it is equal to $L$. We can then write \begin{equation*} mr^2\dot{\theta}=L,\quad \text{or}\quad r\dot{\theta}=\frac{L}{mr}, \end{equation*} and the energy is \begin{equation*} U = \tfrac{1}{2}mv_r^2+V(r)+\frac{L^2}{2mr^2}. \end{equation*} If there were no angular momentum we would have just the first two terms. Adding the angular momentum $L$ does to the energy just what adding a term $L^2/2mr^2$ to the potential energy would do. But this is almost exactly the extra term in (19.46). The only difference is that $l(l+1)\hbar^2$ appears for the angular momentum instead of $l^2\hbar^2$ as we might expect. But we have seen before (for example, Volume II, Section 34-7) that this is just the substitution that is usually required to make a quasi-classical argument agree with a correct quantum-mechanical calculation. We can, then, understand the new term as a “pseudo-potential” which gives the “centrifugal force” term that appears in the equations of radial motion for a rotating system. (See the discussion of “pseudo-forces” in Volume I, Section 12-5.)
We are now ready to solve Eq. (19.46) for $F_l(r)$. It is very much like Eq. (19.8), so the same technique will work again. Everything goes as before until you get to Eq. (19.19) which will have the additional term \begin{equation} \label{Eq:III:19:47} -l(l+1)\sum_{k=1}^\infty a_k\rho^{k-2}. \end{equation} This term can also be written as \begin{equation} \label{Eq:III:19:48} -l(l+1)\biggl\{\frac{a_1}{\rho}+ \sum_{k=1}^\infty a_{k+1}\rho^{k-1}\biggr\}. \end{equation} (We have taken out the first term and then shifted the running index $k$ down by $1$.) Instead of Eq. (19.20) we have \begin{equation} \begin{aligned} \sum_{k=1}^\infty&[\{k(k+1)-l(l+1)\}a_{k+1}-2(\alpha k-1)a_k]\rho^{k-1}\\ &-\frac{l(l+1)a_1}{\rho}=0. \end{aligned} \label{Eq:III:19:49} \end{equation} There is only one term in $\rho^{-1}$, so it must be zero. The coefficient $a_1$ must be zero (unless $l=0$ and we have our previous solution). Each of the other terms is made zero by having the square bracket come out zero for every $k$. This condition replaces Eq. (19.22) by \begin{equation} \label{Eq:III:19:50} a_{k+1}=\frac{2(\alpha k-1)}{k(k+1)-l(l+1)}\,a_k. \end{equation} This is the only significant change from the spherically symmetric case.
As before the series must terminate if we are to have solutions which can represent bound electrons. The series will end at $k=n$ if $\alpha n=1$. We get again the same condition on $\alpha$, that it must be equal to $1/n$, where $n$ is some positive integer. However, Eq. (19.50) also gives a new restriction. The index $k$ cannot be equal to $l$, the denominator becomes zero and $a_{l+1}$ is infinite. That is, since $a_1=0$, Eq. (19.50) implies that all successive $a_k$ are zero until we get to $a_{l+1}$, which can be nonzero. This means that $k$ must start at $l+1$ and end at $n$.
Our final result is that for any $l$ there are many possible solutions which we can call $F_{n,l}$ where $n\geq l+1$. Each solution has the energy \begin{equation} \label{Eq:III:19:51} E_n=-\frac{me^4}{2\hbar^2}\biggl(\frac{1}{n^2}\biggr). \end{equation} The wave function for the state of this energy with the angular quantum numbers $l$ and $m$ is \begin{equation} \label{Eq:III:19:52} \psi_{n,l,m}=a\,Y_{l,m}(\theta,\phi)F_{n,l}(\rho), \end{equation} with \begin{equation} \label{Eq:III:19:53} \rho F_{n,l}(\rho)=e^{-\alpha\rho}\sum_{k=l+1}^na_k\rho^k. \end{equation} The coefficients $a_k$ are obtained from (19.50). We have, finally, a complete description of the states of a hydrogen atom.
19–5The hydrogen wave functions
Let’s review what we have discovered. The states which satisfy Schrödinger’s equation for an electron in a Coulomb field are characterized by three quantum numbers $n$, $l$, $m$, all integers. The angular distribution of the electron amplitude can have only certain forms which we call $Y_{l,m}$. They are labeled by $l$, the quantum number of total angular momentum, and $m$, the “magnetic” quantum number, which can range from $-l$ to $+l$. For each angular configuration, various possible radial distributions $F_{n,l}(r)$ of the electron amplitude are possible; they are labeled by the principal quantum number $n$—which can range from $l+1$ to $\infty$. The energy of the state depends only on $n$, and increases with increasing $n$.
The lowest energy, or ground, state is an $s$-state. It has $l=0$, $n=1$, and $m=0$. It is a “nondegenerate” state—there is only one with this energy, and its wave function is spherically symmetric. The amplitude to find the electron is a maximum at the center, and falls off monotonically with increasing distance from the center. We can visualize the electron amplitude as a blob as shown in Fig. 19–6(a).
There are other $s$-states with higher energies, for $n=2$, $3$, $4$, … For each energy there is only one version ($m=0$), and they are all spherically symmetric. These states have amplitudes which alternate in sign one or more times with increasing $r$. There are $n-1$ spherical nodal surfaces—the places where $\psi$ goes through zero. The $2s$-state ($l=0$, $n=2$), for example, will look as sketched in Fig. 19–6(b). (The dark areas indicate regions where the amplitude is large, and the plus and minus signs indicate the relative phases of the amplitude.) The energy levels of the $s$-states are shown in the first column of Fig. 19–7.
Then there are the $p$-states—with $l=1$. For each $n$, which must be $2$ or greater, there are three states of the same energy, one each for $m=+1$, $m=0$, and $m=-1$. The energy levels are as shown in Fig. 19–7. The angular dependences of these states are given in Table 19–1. For instance, for $m=0$, if the amplitude is positive for $\theta$ near zero, it will be negative for $\theta$ near $180^\circ$. There is a nodal plane coincident with the $xy$-plane. For $n>2$ there are also spherical nodes. The $n=2$, $m=0$ amplitude is sketched in Fig. 19–6(c), and the $n=3$, $m=0$ wave function is sketched in Fig. 19–6(d).
You might think that since $m$ represents a kind of “orientation” in space, there should be similar distributions with the peaks of amplitude along the $x$-axis or along the $y$-axis. Are these perhaps the $m=+1$ and $m=-1$ states? No. But since we have three states with equal energies, any linear combinations of the three will also be stationary states of the same energy. It turns out that the “$x$”-state—which corresponds to the “$z$”-state, or $m=0$ state, of Fig. 19–6(c)—is a linear combination of the $m=+1$ and $m=-1$ states. The corresponding “$y$”-state is another combination. Specifically, we mean that \begin{align*} \text{“$z$”}&=\ket{1,0},\\[1ex] \text{“$x$”}&=-\frac{\ket{1,+1}-\ket{1,-1}}{\sqrt{2}},\\[1ex] \text{“$y$”}&=-\frac{\ket{1,+1}+\ket{1,-1}}{i\sqrt{2}}. \end{align*} These states all look the same when referred to their particular axes.
The $d$-states ($l=2$) have five possible values of $m$ for each energy, the lowest energy has $n=3$. The levels go as shown in Fig. 19–7. The angular dependences get more complicated. For instance the $m=0$ states have two conical nodes, so the wave function reverses phase from $+$, to $-$, to $+$ as you go around from the north pole to the south pole. The rough form of the amplitude is sketched in (e) and (f) of Fig. 19–6 for the $m=0$ states with $n=3$ and $n=4$. Again, the larger $n$’s have spherical nodes.
We will not try to describe any more of the possible states. You will find the hydrogen wave functions described in more detail in many books. Two good references are L. Pauling and E. B. Wilson, Introduction to Quantum Mechanics, McGraw-Hill (1935); and R. B. Leighton, Principles of Modern Physics, McGraw-Hill (1959). You will find in them graphs of some of the functions and pictorial representations of many states.
We would like to mention one particular feature of the wave functions for higher $l$: for $l>0$ the amplitudes are zero at the center. That is not surprising, since it’s hard for an electron to have angular momentum when its radius arm is very small. For this reason, the higher the $l$, the more the amplitudes are “pushed away” from the center. If you look at the way the radial functions $F_{n,l}(r)$ vary for small $r$, you find from (19.53) that \begin{equation*} F_{n,l}(r)\approx r^l. \end{equation*} Such a dependence on $r$ means that for larger $l$’s you have to go farther from $r=0$ before you get an appreciable amplitude. This behavior is, incidentally, determined by the centrifugal force term in the radial equation, so the same thing will apply for any potential that varies slower than $1/r^2$ for small $r$—which most atomic potentials do.
19–6The periodic table
We would like now to apply the theory of the hydrogen atom in an approximate way to get some understanding of the chemist’s periodic table of the elements. For an element with atomic number $Z$ there are $Z$ electrons held together by the electric attraction of the nucleus but with mutual repulsion of the electrons. To get an exact solution we would have to solve Schrödinger’s equation for $Z$ electrons in a Coulomb field. For helium the equation is \begin{equation*} -\frac{\hbar}{i}\ddp{\psi}{t}=-\frac{\hbar^2}{2m} (\nabla_1^2\psi\!+\!\nabla_2^2\psi)\!+\!\biggl(\! -\!\frac{2e^2}{r_1}\!-\!\frac{2e^2}{r_2}\!+\!\frac{e^2}{r_{12}}\!\biggr)\psi, \end{equation*} where $\nabla_1^2$ is a Laplacian which operates on $\FLPr_1$, the coordinate of one electron; $\nabla_2^2$ operates on $\FLPr_2$; and $r_{12}=\abs{\FLPr_1-\FLPr_2}$. (We are again neglecting the spin of the electrons.) To find the stationary states and energy levels we would have to find solutions of the form \begin{equation*} \psi=f(\FLPr_1,\FLPr_2)e^{-(i/\hbar)Et}. \end{equation*} The geometrical dependence is contained in $f$, which is a function of six variables—the simultaneous positions of the two electrons. No one has found an analytic solution, although solutions for the lowest energy states have been obtained by numerical methods.
With $3$, $4$, or $5$ electrons it is hopeless to try to obtain exact solutions, and it is going too far to say that quantum mechanics has given a precise understanding of the periodic table. It is possible, however, even with a sloppy approximation—and some fixing—to understand, at least qualitatively, many chemical properties which show up in the periodic table.
The chemical properties of atoms are determined primarily by their lowest energy states. We can use the following approximate theory to find these states and their energies. First, we neglect the electron spin, except that we adopt the exclusion principle and say that any particular electronic state can be occupied by only one electron. This means that any particular orbital configuration can have up to two electrons—one with spin up, the other with spin down. Next we disregard the details of the interactions between the electrons in our first approximation, and say that each electron moves in a central field which is the combined field of the nucleus and all the other electrons. For neon, which has $10$ electrons, we say that one electron sees an average potential due to the nucleus plus the other nine electrons. We imagine then that in the Schrödinger equation for each electron we put a $V(r)$ which is a $1/r$ field modified by a spherically symmetric charge density coming from the other electrons.
In this model each electron acts like an independent particle. The angular dependence of its wave function will be just the same as the ones we had for the hydrogen atom. There will be $s$-states, $p$-states, and so on; and they will have the various possible $m$-values. Since $V(r)$ no longer goes as $1/r$, the radial part of the wave functions will be somewhat different, but it will be qualitatively the same, so we will have the same radial quantum numbers, $n$. The energies of the states will also be somewhat different.
With these ideas, let’s see what we get. The ground state of hydrogen has $l=m=0$ and $n=1$; we say the electron configuration is $1s$. The energy is $-13.6$ eV. This means that it takes $13.6$ electron volts to pull the electron off the atom. We call this the “ionization energy”, $W_I$. A large ionization energy means that it is harder to pull the electron off and, in general, that the material is chemically less active.
Now take helium. Both electrons can be in the same lowest state (one spin up and the other spin down). In this lowest state the electron moves in a potential which is for small $r$ like a Coulomb field for $z=2$ and for large $r$ like a Coulomb field for $z=1$. The result is a “hydrogen-like” $1s$ state with a somewhat lower energy. Both electrons occupy identical $1s$ states ($l=0$, $m=0$). The observed ionization energy (to remove one electron) is $24.6$ electron volts. Since the $1s$ “shell” is now filled—we allow only two electrons—there is practically no tendency for an electron to be attracted from another atom. Helium is chemically inert.
The lithium nucleus has a charge of $3$. The electron states will again be hydrogen-like, and the three electrons will occupy the lowest three energy levels. Two will go into $1s$ states and the third will go into an $n=2$ state. But with $l=0$ or $l=1$? In hydrogen these states have the same energy, but in other atoms they don’t, for the following reason. Remember that a $2s$ state has some amplitude to be near the nucleus while the $2p$ state does not. That means that a $2s$ electron will feel some of the triple electric charge of the Li nucleus, but that a $2p$ electron will stay out where the field looks like the Coulomb field of a single charge. The extra attraction lowers the energy of the $2s$ state relative to the $2p$ state. The energy levels will be roughly as shown in Fig. 19–8—which you should compare with the corresponding diagram for hydrogen in Fig. 19–7. So the lithium atom will have two electrons in $1s$ states and one in a $2s$. Since the $2s$ electron has a higher energy than a $1s$ electron it is relatively easily removed. The ionization energy of lithium is only $5.4$ electron volts, and it is quite active chemically.
So you can see the patterns which develop; we have given in Table 19–2 a list of the first $36$ elements, showing the states occupied by the electrons in the ground state of each atom. The Table gives the ionization energy for the most loosely bound electron, and the number of electrons occupying each “shell”—by which we mean states with the same $n$. Since the different $l$-states have different energies, each $l$-value corresponds to a sub-shell of $2(2l+1)$ possible states (of different $m$ and electron spin). These all have the same energy—except for some very small effects we are neglecting.
| $Z$ | Element | $W_I(eV)$ | Electron Configuration | ||||||||||
| $1s$ | $2s$ | $2p$ | $3s$ | $3p$ | $3d$ | $4s$ | $4p$ | $4d$ | $4f$ | ||||
| $1$ | H | hydrogen | $13.6$ | $1$ | |||||||||
| $2$ | He | helium | $24.6$ | $2$ | |||||||||
| $3$ | Li | lithium | $5.4$ | FILLED $(2)$ |
$1$ | ||||||||
| $4$ | Be | beryllium | $9.3$ | $2$ | |||||||||
| $5$ | B | boron | $8.3$ | $2$ | $1$ | ||||||||
| $6$ | C | carbon | $11.3$ | $2$ | $2$ | Number of electrons in each state | |||||||
| $7$ | N | nitrogen | $14.5$ | $2$ | $3$ | ||||||||
| $8$ | O | oxygen | $13.6$ | $2$ | $4$ | ||||||||
| $9$ | F | fluorine | $17.4$ | $2$ | $5$ | ||||||||
| $10$ | Ne | neon | $21.6$ | $2$ | $6$ | ||||||||
| $11$ | Na | sodium | $5.1$ | $1$ | |||||||||
| $12$ | Mg | magnesium | $7.6$ | $2$ | |||||||||
| $13$ | Al | aluminum | $6.0$ | $2$ | $1$ | ||||||||
| $14$ | Si | silicon | $8.1$ | —FILLED— | $2$ | $2$ | |||||||
| $15$ | P | phosphorus | $10.5$ | $2$ | $3$ | ||||||||
| $16$ | S | sulfur | $10.4$ | $(2)$ | $(8)$ | $2$ | $4$ | ||||||
| $17$ | Cl | chlorine | $13.0$ | $2$ | $5$ | ||||||||
| $18$ | Ar | argon | $15.8$ | $2$ | $6$ | ||||||||
| $19$ | K | potassium | $4.3$ | $1$ | |||||||||
| $20$ | Ca | calcium | $6.1$ | $2$ | |||||||||
| $21$ | Sc | scandium | $6.5$ | $\phantom{1}1$ | $2$ | ||||||||
| $22$ | Ti | titanium | $6.8$ | $\phantom{1}2$ | $2$ | ||||||||
| $23$ | V | vanadium | $6.7$ | ——FILLED—— | $\phantom{1}3$ | $2$ | |||||||
| $24$ | Cr | chromium | $6.8$ | $\phantom{1}5$ | $1$ | ||||||||
| $25$ | Mn | manganese | $7.4$ | $(2)$ | $(8)$ | $(8)$ | $\phantom{1}5$ | $2$ | |||||
| $26$ | Fe | iron | $7.9$ | $\phantom{1}6$ | $2$ | ||||||||
| $27$ | Co | cobalt | $7.9$ | $\phantom{1}7$ | $2$ | ||||||||
| $28$ | Ni | nickel | $7.6$ | $\phantom{1}8$ | $2$ | ||||||||
| $29$ | Cu | copper | $7.7$ | $10$ | $1$ | ||||||||
| $30$ | Zn | zinc | $9.4$ | $10$ | $2$ | ||||||||
| $31$ | Ga | gallium | $6.0$ | $2$ | $1$ | ||||||||
| $32$ | Ge | germanium | $7.9$ | ——FILLED—— | $2$ | $2$ | |||||||
| $33$ | As | arsenic | $9.8$ | $2$ | $3$ | ||||||||
| $34$ | Se | selenium | $9.7$ | $(2)$ | $(8)$ | $(18)$ | $2$ | $4$ | |||||
| $35$ | Br | bromine | $11.8$ | $2$ | $5$ | ||||||||
| $36$ | Kr | krypton | $14.0$ | $2$ | $6$ | ||||||||
Beryllium is like lithium except that it has two electrons in the $2s$ state as well as two in the filled $1s$ shell.
Boron has $5$ electrons. The fifth must go into a $2p$ state. There are $2\times3=6$ different $2p$ states, so we can keep adding electrons until we get to a total of $8$. This takes us to neon. As we add these electrons we are also increasing $Z$, so the whole electron distribution gets pulled in closer and closer to the nucleus and the energy of the $2p$ states goes down. By the time we get to neon the ionization energy is up to $21.6$ electron volts. Neon does not easily give up an electron. Also there are no more low-energy slots to be filled, so it won’t try to grab an extra electron. Neon is chemically inert. Fluorine, on the other hand, does have an empty position where an electron can drop into a state of low energy, so it is quite active in chemical reactions.
With sodium the eleventh electron must start a new shell—going into a $3s$ state. The energy level of this state is much higher; the ionization energy jumps down; and sodium is an active chemical. From sodium to argon the $s$ and $p$ states with $n=3$ are occupied in exactly the same sequence as for lithium to neon. Angular configurations of the electrons in the outer unfilled shell have the same sequence, and the progression of ionization energies is quite similar. You can see why the chemical properties repeat with increasing atomic number. Magnesium acts chemically much like beryllium, silicon like carbon, and chlorine like fluorine. Argon is inert like neon.
You may have noticed that there is a slight peculiarity in the sequence of ionization energies between lithium and neon, and a similar one between sodium and argon. The last electron is bound to the oxygen atom somewhat less than we might expect. And sulfur is similar. Why should that be? We can understand it if we put in just a little bit of the effects of the interactions between individual electrons. Think of what happens when we put the first $2p$ electron onto the boron atom. It has six possibilities—three possible $p$-states, each with two spins. Imagine that the electron goes with spin up into the $m=0$ state, which we have also called the “$z$” state because it hugs the $z$-axis. Now what will happen in carbon? There are now two $2p$ electrons. If one of them goes into the “$z$” state, where will the second one go? It will have lower energy if it stays away from the first electron, which it can do by going into, say, the “$x$” state of the $2p$ shell. (This state is, remember, just a linear combination of the $m=+1$ and $m=-1$ states.) Next, when we go to nitrogen, the three $2p$ electrons will have the lowest energy of mutual repulsion if they go one each into the “$x$,” “$y$,” and “$z$” configurations. For oxygen, however, the jig is up. The fourth electron must go into one of the filled states—with opposite spin. It is strongly repelled by the electron already in that state, so its energy will not be as low as it might otherwise be, and it is more easily removed. That explains the break in the sequence of binding energies which appears between nitrogen and oxygen, and between phosphorus and sulfur.
After argon, you would, at first, think that the new electrons would start to fill up the $3d$ states. But they don’t. As we described earlier—and illustrated in Fig. 19–8—the higher angular momentum states get pushed up in energy. By the time we get to the $3d$ states they are pushed to an energy a little bit above the energy of the $4s$ state. So in potassium the last electron goes into the $4s$ state. After this shell is filled (with two electrons) at calcium, the $3d$ states begin to be filled for scandium, titanium, and vanadium.
The energies of the $3d$ and $4s$ states are so close together that small effects can shift the balance either way. By the time we get to put four electrons into the $3d$ states, their repulsion raises the energy of the $4s$ state just enough that its energy is slightly above the $3d$ energy, so one electron shifts over. For chromium we don’t get a $4$, $2$ combination as we would have expected, but instead a $5$, $1$ combination. The new electron added to get manganese fills up the $4s$ shell again, and the states of the $3d$ shell are then occupied one by one until we reach copper.
Since the outermost shell of manganese, iron, cobalt, and nickel have the same configurations, however, they all tend to have similar chemical properties. (This effect is much more pronounced in the rare-earth elements which all have the same outer shell but a progressively filling inner shell which has much less influence on their chemical properties.)
In copper an electron is robbed from the $4s$ shell, finally completing the $3d$ shell. The energy of the $10$, $1$ combination is, however, so close to the $9$, $2$ configuration for copper that just the presence of another atom nearby can shift the balance. For this reason the two last electrons of copper are nearly equivalent, and copper can have a valence of either $1$ or $2$. (It sometimes acts as though its electrons were in the $9$, $2$ combination.) Similar things happen at other places and account for the fact that other metals, such as iron, combine chemically with either of two valences. By zinc, both the $3d$ and $4s$ shells are filled once and for all.
From gallium to krypton the sequence proceeds normally again, filling the $4p$ shell. The outer shells, the energies, and the chemical properties repeat the pattern of boron to neon and aluminum to argon.
Krypton, like argon and neon, is known as “noble” gas. All three are chemically “inert.” This means only that, having filled shells of relatively low energy, there are few situations in which there is an energy advantage for them to join in a simple combination with other elements. Having a filled shell is not enough. Beryllium and magnesium have filled $s$-shells, but the energy of these shells is too high to lead to stability. Similarly, one would have expected another “noble” element at nickel, if the energy of the $3d$ shell had been lower (or the $4s$ higher). On the other hand, krypton is not completely inert; it will form a weakly-bound compound with chlorine.
Since our sample has turned up most of the main features of the periodic table, we stop our examination at element number $36$—there are still seventy or so more!
We would like to bring up only one more point—that we not only can understand the valences to some extent but also can say something about the directional properties of the chemical bonds. Take an atom like oxygen which has four $2p$ electrons. The first three go into “$x$,” “$y$,” and “$z$” states and the fourth will double one of these states, leaving two—say “$x$” and “$y$”—vacant. Consider then what happens in H$_2$O. Each of the two hydrogens are willing to share an electron with the oxygen, helping the oxygen to fill a shell. These electrons will tend to go into the “$x$” and “$y$” vacancies. So the water molecule should have the two hydrogen atoms making a right angle with respect to the center of the oxygen. The angle is actually $105^\circ$. We can even understand why the angle is larger than $90^\circ$. In sharing their electrons the hydrogens end up with a net positive charge. The electric repulsion “strains” the wave functions and pushes the angle out to $105^\circ$. The same situation occurs in H$_2$S. But because the sulfur atom is larger, the two hydrogen atoms are farther apart, there is less repulsion, and the angle is only pushed out to about $93^\circ$. Selenium is even larger, so in H$_2$Se the angle is very nearly $90^\circ$.
We can use the same arguments to understand the geometry of ammonia, H$_3$N. Nitrogen has room for three more $2p$ electrons, one each for the “$x$,” “$y$,” and “$z$” type states. The three hydrogens should join on at right angles to each other. The angles come out a little larger than $90^\circ$—again from the electric repulsion—but at least we see why the molecule of H$_3$N is not flat. The angles in phosphene, H$_3$P, are close to $90^\circ$, and in H$_3$As are still closer. We assumed that NH$_3$ was not flat when we described it as a two-state system. And the nonflatness is what makes the ammonia maser possible. Now we see that also that shape can be understood from our quantum mechanics.
The Schrödinger equation has been one of the great triumphs of physics. By providing the key to the underlying machinery of atomic structure it has given an explanation for atomic spectra, for chemistry, and for the nature of matter.
- As usual, $e^2=q_e^2/4\pi\epsO$. ↩
- Since these special names are part of the common vocabulary of atomic physics, you will just have to learn them. We will help out by putting them together in a short “dictionary” later in the chapter. ↩
- You can with some work show that this comes out of Eq. (18.35), but it is also easy to work out from first principles following the ideas of Section 18-4. A state $\ket{l,l}$ can be made out of $2l$ spin one-half particles all with spins up; while the state $\ket{l,0}$ would have $l$ up and $l$ down. Under the rotation the amplitude that an up-spin remains up is $\cos\theta/2$, and that an up-spin goes down is $-\sin\theta/2$. We are asking for the amplitude that $l$ up-spins stay up, while the other $l$ up-spins go down. The amplitude for that is $(-\cos\theta/2 \sin\theta/2)^l$ which is proportional to $\sin^l\theta$. ↩