1. I sent M. Atiyah this paper and he replied with the paper, Complex Geometry of Nuclei and Atoms

2. Addendum: Making a drug without side effects(Sep. 18 2019)
We make the following claims which came up while working on the note, For quantum mechanical model on decision making

(1) A molecule such as enzymes, proteins has an oscillator activated by a unique 'resonance' frequency(or oscillators, see for superposition).
For, the amplitude x of an oscillator is governed by the equation \begin{equation} m\frac{d^2x}{dt^2}+c\frac{dx}{dt}+kx=F_0 \cos(\omega t+\Delta), c=m\gamma, k=m{\omega_0}^2 \end{equation}
and the solution is given as $x=\rho F_0\cos(\omega t+\Delta+\theta) $ and the relation between ${\rho}^2$ and frequecy is as follows.

Adapted from Feynman Lectures on Physics, Vol I

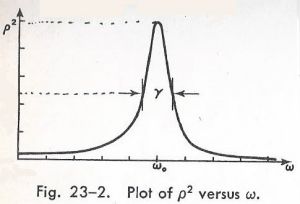
$\Delta \omega=\gamma$ when $\gamma$ is small, which implies that a molecule is activated by a frequency 'very close' to the resonance frequency $\omega_0$ (Refer to [1] and see also a induced precession) This explains why such molecules work with high-precision, just as a right tune can hear a specific station broadcast.

This claim could be proved like this. Mix two different-type enzymes, put it under an electric field and seperate into two group by varying frequencies of the electric field(for some sort of evidence, Jul. 11 2021)

(2) The 'resonance' frequency concept suggests a way of making a drug which manages to find a specific cell only, which means a drug without side effects. For example, a cancer cell would radiate a different wave from the one from a normal cell(Refer to [2]). So make a molecule activating by the wave of a cencer cell(i.e. a carrier to a cencer cell) and attach to a drug.

(3) On how enzymes work, roughly speaking, wake up by a unique frequency => activate a motor moving towards a specific target => associate with the target and make change of free electrons distribution.

[1] Feynman Lectures on Physics, Vol I, 23-6
[2] Feynman Lectures on Physics, Vol I 28-4